scipy.spatial.

HalfspaceIntersection

class scipy.spatial.HalfspaceIntersection(halfspaces, interior_point, incremental=False, qhull_options=None)

N 维半空间交集。

0.19.0 版本新增。

参数:

halfspaces浮点型 ndarray，形状 (nineq, ndim+1)

Ax + b <= 0 形式的堆叠不等式，格式为 [A; b]

interior_point浮点型 ndarray，形状 (ndim,)

明确位于半空间定义区域内的点。也称为可行点，可以通过线性规划获得。

incremental布尔型，可选

允许增量添加新的半空间。这会占用一些额外资源。

qhull_options字符串，可选

传递给 Qhull 的额外选项。详见 Qhull 手册。（默认：ndim > 4 时为“Qx”，否则为空字符串）选项“H”始终启用。

属性:

halfspaces双精度浮点型 ndarray，形状 (nineq, ndim+1)

输入的半空间。

interior_point :浮点型 ndarray，形状 (ndim,)

输入的内部点。

intersections双精度浮点型 ndarray，形状 (ninter, ndim)

所有半空间的交点。

dual_points双精度浮点型 ndarray，形状 (nineq, ndim)

输入半空间的对偶点。

dual_facets整数列表的列表

构成对偶凸包的（不一定是单形的）面的点索引。

dual_vertices整数型 ndarray，形状 (nvertices,)

构成对偶凸包顶点的半空间索引。对于二维凸包，顶点按逆时针顺序排列。对于其他维度，它们按输入顺序排列。

dual_equations双精度浮点型 ndarray，形状 (nfacet, ndim+1)

[法向量，偏移] 构成对偶面的超平面方程（详见 Qhull 文档）。

dual_area浮点型

对偶凸包的面积

dual_volume浮点型

对偶凸包的体积

方法

add_halfspaces(halfspaces[, restart])	处理一组额外的新半空间。
close()	完成增量处理。

引发:

QhullError

当 Qhull 遇到错误条件时引发，例如未启用解决选项时的几何退化。

ValueError

如果输入不兼容的数组则引发。

备注

交集是使用 Qhull 库 计算的。这重现了 Qhull 的“qhalf”功能。

参考文献

[Qhull]

http://www.qhull.org/

[1]

S. Boyd, L. Vandenberghe, Convex Optimization，可在此处获取：http://stanford.edu/~boyd/cvxbook/

示例

在浏览器中尝试！

形成多边形的半空间交集

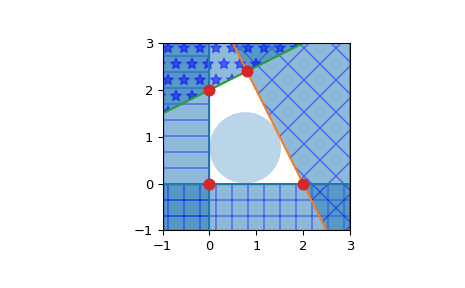
>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

将半空间绘制为填充区域和交点

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1, aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

默认情况下，Qhull 不提供计算内部点的方法。这可以通过线性规划轻松计算。考虑 \(Ax + b \leq 0\) 形式的半空间，求解线性规划

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

其中 \(A_i\) 是 A 的行，即每个平面的法向量。

这将产生一个位于凸多面体内部最深处的点 x。确切地说，它是内切于多面体的最大半径为 y 的超球体中心。这个点被称为多面体的切比雪夫中心（参见 [1] 4.3.1, pp148-149）。Qhull 输出的方程总是归一化的。

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b, bounds=(None, None))
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()

返回在新标签页中打开