firwin_2d#
- scipy.signal.firwin_2d(hsize, window, *, fc=None, fs=2, circular=False, pass_zero=True, scale=True)[source]#
使用窗函数法设计二维 FIR 滤波器。
此函数计算二维有限脉冲响应滤波器的系数。该滤波器是具有线性相位的可分离滤波器;它将被设计为两个一维滤波器的乘积,其维度由 hsize 定义。此外,它可以创建近似圆对称的二维窗函数。
- 参数:
- hsize长度为 2 的元组或列表
滤波器在每个维度上的长度。hsize[0] 指定行方向的系数数量,hsize[1] 指定列方向的系数数量。
- window长度为 2 的元组或列表,或字符串
用于每个一维滤波器的期望窗函数,或用于创建圆对称二维窗函数的单一窗函数类型。每个元素应为字符串或字符串和参数值的元组。有关窗函数列表和所需参数,请参阅
get_window。- fc浮点数或一维类数组,可选
滤波器截止频率,单位与 fs 相同。这定义了低通或高通滤波器中,滤波器增益降至约 -6 dB(半功率)的频率。对于多频带滤波器,fc 可以是截止频率(即频带边缘)数组,范围为 [0, fs/2],每个频带以对形式指定。circular 为 False 时必需。
- fs浮点数,可选
信号的采样频率。默认为 2。
- circular布尔值,可选
是否创建圆对称二维窗函数。默认为
False。- pass_zero{True, False, ‘bandpass’, ‘lowpass’, ‘highpass’, ‘bandstop’},可选
此参数直接传递给每个标量频率轴的
firwin。因此,如果为True,则 DC 增益,即频率 (0, 0) 处的增益为 1。如果为False,则当 circular 为True时,频率 (0, 0) 处的 DC 增益为 0。如果 circular 为False,则频率 (0, f1) 和 (f0, 0) 将具有 0 增益。它也可以是所需滤波器类型的字符串参数(等同于 IIR 设计函数中的btype)。- scale布尔值,可选
此参数直接传递给每个标量频率轴的
firwin。设置为True以按比例缩放系数,使频率响应在某个频率轴上的特定频率处恰好为单位增益。该频率为如果第一个通带从 0 开始(即 pass_zero 为
True),则为 0 (DC)如果第一个通带在 fs/2 结束(即滤波器是单频带高通滤波器),则为 fs/2(奈奎斯特频率);否则为第一个通带的中心
- 返回:
- filter_2d(hsize[0], hsize[1]) ndarray
二维 FIR 滤波器的系数。
- 引发:
- ValueError
如果 hsize 和 window 不是两个元素的元组或列表。
如果 circular 为 True 时 cutoff 为 None。
如果 circular 为
False且 cutoff 超出范围 [0, fs/2]。如果 window 中的任何元素无法识别。
- RuntimeError
如果
firwin在设计滤波器时未能收敛。
另请参阅
firwin使用窗函数法设计一维数组的 FIR 滤波器。
get_window返回给定长度和类型的窗函数。
示例
生成一个截止频率为 0.1 的 5x5 低通滤波器
>>> import numpy as np >>> from scipy.signal import get_window >>> from scipy.signal import firwin_2d >>> hsize = (5, 5) >>> window = (("kaiser", 5.0), ("kaiser", 5.0)) >>> fc = 0.1 >>> filter_2d = firwin_2d(hsize, window, fc=fc) >>> filter_2d array([[0.00025366, 0.00401662, 0.00738617, 0.00401662, 0.00025366], [0.00401662, 0.06360159, 0.11695714, 0.06360159, 0.00401662], [0.00738617, 0.11695714, 0.21507283, 0.11695714, 0.00738617], [0.00401662, 0.06360159, 0.11695714, 0.06360159, 0.00401662], [0.00025366, 0.00401662, 0.00738617, 0.00401662, 0.00025366]])
生成一个使用 Hamming 窗函数的圆对称 5x5 低通滤波器
>>> filter_2d = firwin_2d((5, 5), 'hamming', fc=fc, circular=True) >>> filter_2d array([[-0.00020354, -0.00020354, -0.00020354, -0.00020354, -0.00020354], [-0.00020354, 0.01506844, 0.09907658, 0.01506844, -0.00020354], [-0.00020354, 0.09907658, -0.00020354, 0.09907658, -0.00020354], [-0.00020354, 0.01506844, 0.09907658, 0.01506844, -0.00020354], [-0.00020354, -0.00020354, -0.00020354, -0.00020354, -0.00020354]])
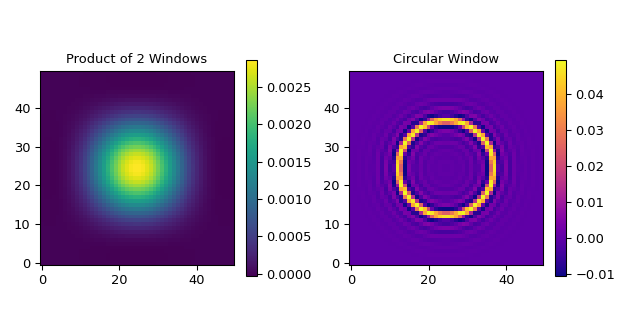
生成比较两个一维滤波器乘积与圆对称滤波器的图
>>> import matplotlib.pyplot as plt >>> hsize, fc = (50, 50), 0.05 >>> window = (("kaiser", 5.0), ("kaiser", 5.0)) >>> filter0_2d = firwin_2d(hsize, window, fc=fc) >>> filter1_2d = firwin_2d((50, 50), 'hamming', fc=fc, circular=True) ... >>> fg, (ax0, ax1) = plt.subplots(1, 2, tight_layout=True, figsize=(6.5, 3.5)) >>> ax0.set_title("Product of 2 Windows") >>> im0 = ax0.imshow(filter0_2d, cmap='viridis', origin='lower', aspect='equal') >>> fg.colorbar(im0, ax=ax0, shrink=0.7) >>> ax1.set_title("Circular Window") >>> im1 = ax1.imshow(filter1_2d, cmap='plasma', origin='lower', aspect='equal') >>> fg.colorbar(im1, ax=ax1, shrink=0.7) >>> plt.show()