envelope#
- scipy.signal.envelope(z, bp_in=(1, None), *, n_out=None, squared=False, residual='lowpass', axis=-1)[源码]#
计算实值或复值信号的包络。
- 参数:
- zndarray
实值或复值输入信号,假定由
n个样本组成,采样间隔为T。 z 也可以是多维数组,其中时间轴由 axis 定义。- bp_intuple[int | None, int | None],可选
定义输入滤波器频率带
bp_in[0]:bp_in[1]的 2 元组。角频率指定为1/(n*T)的整数倍,其中-n//2 <= bp_in[0] < bp_in[1] <= (n+1)//2是允许的频率范围。None条目分别替换为-n//2或(n+1)//2。默认值(1, None)移除平均值以及负频率分量。- n_outint | None,可选
如果不是
None,输出将被重新采样到 n_out 个样本。默认值None将输出设置为与输入 z 相同的长度。- squaredbool,可选
如果设置,返回包络的平方。由于所用绝对值函数的非线性特性,平方包络的带宽通常小于非平方包络的带宽。即,嵌入的平方根函数通常会产生额外的谐波。默认值为
False。- residualLiteral[‘lowpass’, ‘all’, None],可选
此选项确定返回何种残余信号,即输入带通滤波器移除的信号部分。
'all'返回频率带bp_in[0]:bp_in[1]之外的所有内容,'lowpass'返回频率带< bp_in[0]的内容。如果为None,则只返回包络。默认值:'lowpass'。- axisint,可选
计算包络时 z 的轴。默认是最后一个轴。
- 返回:
- ndarray
如果参数 residual 为
None,则返回一个与输入 z 形状相同的数组z_env,其中包含其包络。否则,返回一个形状为(2, *z.shape)的数组,其中包含沿第一个轴堆叠的数组z_env和z_res。它允许解包,例如z_env, z_res = envelope(z, residual='all')。残余信号z_res包含输入带通滤波器移除的信号部分,具体取决于参数 residual。请注意,对于实值信号,返回实值残余信号。因此,bp_in 的负频率分量将被忽略。
另请参阅
hilbert通过希尔伯特变换计算解析信号。
注意
任何复值信号 \(z(t)\) 可以由实值瞬时幅度 \(a(t)\) 和实值瞬时相位 \(\phi(t)\) 描述,即 \(z(t) = a(t) \exp\!\big(j \phi(t)\big)\)。包络被定义为幅度的绝对值 \(|a(t)| = |z(t)|\),它同时也是信号的绝对值。因此,\(|a(t)|\) “包络”了所有具有幅度 \(a(t)\) 和任意相位 \(\phi(t)\) 的信号类别。对于实值信号,\(x(t) = a(t) \cos\!\big(\phi(t)\big)\) 是类比的公式。因此,\(|a(t)|\) 可以通过希尔伯特变换将 \(x(t)\) 转换为解析信号 \(z_a(t)\) 来确定,即 \(z_a(t) = a(t) \cos\!\big(\phi(t)\big) + j a(t) \sin\!\big(\phi(t) \big)\),这将产生一个具有相同包络 \(|a(t)|\) 的复值信号。
该实现基于计算输入信号的 FFT,然后在傅里叶空间执行必要的操作。因此,需要考虑典型的 FFT 注意事项:
信号假定为周期性的。信号开始和结束之间的不连续性可能因吉布斯现象导致不理想的结果。
如果信号长度是素数或非常长,FFT 会很慢。此外,内存需求通常高于基于 FIR/IIR 滤波器的可比较实现。
带通滤波器角频率的频率间隔
1 / (n*T)对应于scipy.fft.fftfreq(len(z), T)产生的频率。
如果需要不带通滤波的复值信号 z 的包络,即
bp_in=(None, None),则包络对应于绝对值。因此,使用np.abs(z)比使用此函数更高效。尽管基于解析信号 [1] 计算包络是实值信号的自然方法,但其他方法也经常使用。最流行的替代方法可能是所谓的“平方律”包络检波器及其相关方法 [2]。它们并非总是能计算出所有类型信号的正确结果,但对于大多数窄带信号通常是正确的,并且计算效率更高。此处提出的包络定义在瞬时幅度和相位受到关注时很常见(例如,如 [3] 中所述)。还存在其他依赖于包络的一般数学思想的概念 [4]:一种实用的方法是确定所有信号的上限和下限峰值,并使用样条插值来确定曲线 [5]。
参考文献
[1]“解析信号”,维基百科,https://en.wikipedia.org/wiki/Analytic_signal
[4]“包络(数学)”,维基百科,https://en.wikipedia.org/wiki/Envelope_(mathematics)
示例
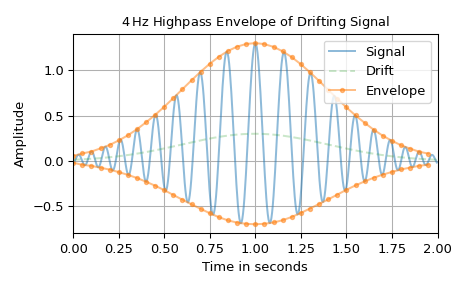
以下图表说明了具有可变频率和低频漂移的信号包络。为了将漂移与包络分离,使用了 4 Hz 高通滤波器。输入带通滤波器的低通残余用于确定非对称的上限和下限以包围信号。由于所得包络的平滑性,它从 500 个样本下采样到 40 个样本。请注意,瞬时幅度
a_x和计算出的包络x_env并非完全相同。这是因为信号并非完全周期性,以及x_carrier和x_drift存在一些频谱重叠。因此,它们不能通过带通滤波器完全分离。>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.signal.windows import gaussian >>> from scipy.signal import envelope ... >>> n, n_out = 500, 40 # number of signal samples and envelope samples >>> T = 2 / n # sampling interval for 2 s duration >>> t = np.arange(n) * T # time stamps >>> a_x = gaussian(len(t), 0.4/T) # instantaneous amplitude >>> phi_x = 30*np.pi*t + 35*np.cos(2*np.pi*0.25*t) # instantaneous phase >>> x_carrier = a_x * np.cos(phi_x) >>> x_drift = 0.3 * gaussian(len(t), 0.4/T) # drift >>> x = x_carrier + x_drift ... >>> bp_in = (int(4 * (n*T)), None) # 4 Hz highpass input filter >>> x_env, x_res = envelope(x, bp_in, n_out=n_out) >>> t_out = np.arange(n_out) * (n / n_out) * T ... >>> fg0, ax0 = plt.subplots(1, 1, tight_layout=True) >>> ax0.set_title(r"$4\,$Hz Highpass Envelope of Drifting Signal") >>> ax0.set(xlabel="Time in seconds", xlim=(0, n*T), ylabel="Amplitude") >>> ax0.plot(t, x, 'C0-', alpha=0.5, label="Signal") >>> ax0.plot(t, x_drift, 'C2--', alpha=0.25, label="Drift") >>> ax0.plot(t_out, x_res+x_env, 'C1.-', alpha=0.5, label="Envelope") >>> ax0.plot(t_out, x_res-x_env, 'C1.-', alpha=0.5, label=None) >>> ax0.grid(True) >>> ax0.legend() >>> plt.show()
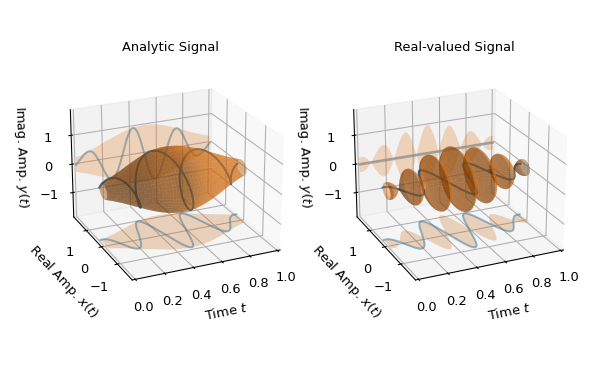
第二个示例提供了复值信号的几何包络解释:以下两个图显示了复值信号为蓝色 3D 轨迹,包络为橙色圆形管,直径可变,即 \(|a(t)| \exp(j\rho(t))\),其中 \(\rho(t)\in[-\pi,\pi]\)。此外,还描绘了轨迹和管在 2D 实部和虚部坐标平面上的投影。复值信号的每个点都接触管的表面。
左图显示了解析信号,即虚部和实部之间的相位差始终为 90 度,从而形成螺旋轨迹。可以看出,在这种情况下,实部也具有预期的包络,即表示瞬时幅度的绝对值。
右图显示了该解析信号的实部被解释为复值信号,即虚部为零。在这种情况下,得到的包络不像解析情况下那样平滑,并且实平面中的瞬时幅度未被恢复。如果
z_re作为实值信号传递,即作为z_re = z.real而不是z_re = z.real + 0j,则结果将与左图相同。这样做的原因是实值信号被解释为复值解析信号的实部。>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.signal.windows import gaussian >>> from scipy.signal import envelope ... >>> n, T = 1000, 1/1000 # number of samples and sampling interval >>> t = np.arange(n) * T # time stamps for 1 s duration >>> f_c = 3 # Carrier frequency for signal >>> z = gaussian(len(t), 0.3/T) * np.exp(2j*np.pi*f_c*t) # analytic signal >>> z_re = z.real + 0j # complex signal with zero imaginary part ... >>> e_a, e_r = (envelope(z_, (None, None), residual=None) for z_ in (z, z_re)) ... >>> # Generate grids to visualize envelopes as 2d and 3d surfaces: >>> E2d_t, E2_amp = np.meshgrid(t, [-1, 1]) >>> E2d_1 = np.ones_like(E2_amp) >>> E3d_t, E3d_phi = np.meshgrid(t, np.linspace(-np.pi, np.pi, 300)) >>> ma = 1.8 # maximum axis values in real and imaginary direction ... >>> fg0 = plt.figure(figsize=(6.2, 4.)) >>> ax00 = fg0.add_subplot(1, 2, 1, projection='3d') >>> ax01 = fg0.add_subplot(1, 2, 2, projection='3d', sharex=ax00, ... sharey=ax00, sharez=ax00) >>> ax00.set_title("Analytic Signal") >>> ax00.set(xlim=(0, 1), ylim=(-ma, ma), zlim=(-ma, ma)) >>> ax01.set_title("Real-valued Signal") >>> for z_, e_, ax_ in zip((z, z.real), (e_a, e_r), (ax00, ax01)): ... ax_.set(xlabel="Time $t$", ylabel="Real Amp. $x(t)$", ... zlabel="Imag. Amp. $y(t)$") ... ax_.plot(t, z_.real, 'C0-', zs=-ma, zdir='z', alpha=0.5, label="Real") ... ax_.plot_surface(E2d_t, e_*E2_amp, -ma*E2d_1, color='C1', alpha=0.25) ... ax_.plot(t, z_.imag, 'C0-', zs=+ma, zdir='y', alpha=0.5, label="Imag.") ... ax_.plot_surface(E2d_t, ma*E2d_1, e_*E2_amp, color='C1', alpha=0.25) ... ax_.plot(t, z_.real, z_.imag, 'C0-', label="Signal") ... ax_.plot_surface(E3d_t, e_*np.cos(E3d_phi), e_*np.sin(E3d_phi), ... color='C1', alpha=0.5, shade=True, label="Envelope") ... ax_.view_init(elev=22.7, azim=-114.3) >>> fg0.subplots_adjust(left=0.08, right=0.97, wspace=0.15) >>> plt.show()