scipy.differentiate.

derivative#

scipy.differentiate.derivative(f, x, *, args=(), tolerances=None, maxiter=10, order=8, initial_step=0.5, step_factor=2.0, step_direction=0, preserve_shape=False, callback=None)[源代码]#

数值计算逐元素实标量函数的导数。

对于f输出的每个元素，scipy.differentiate.derivative 使用有限差分法近似计算f在x的对应元素处的一阶导数。

当x、step_direction和args包含（可广播的）数组时，此函数逐元素工作。

参数：
f可调用对象

需要计算导数的函数。其签名必须是

f(xi: ndarray, *argsi) -> ndarray

其中xi的每个元素都是一个有限实数，而argsi是一个元组，可能包含任意数量可与xi广播的数组。f必须是一个逐元素函数：对于有效索引j，f(xi)[j]的每个标量元素必须等于f(xi[j])。它不得修改数组xi或argsi中的数组。

x浮点型类数组

计算导数的横坐标。必须可与args和step_direction广播。

args类数组元组，可选

要传递给f的额外位置数组参数。数组必须彼此以及与init的数组可广播。如果所需根的可调用对象需要与x不可广播的参数，则将该可调用对象用f包装，使f只接受x和可广播的*args。

tolerances浮点数字典，可选

绝对和相对容差。字典的有效键为

  • atol - 导数的绝对容差

  • rtol - 导数的相对容差

当res.error < atol + rtol * abs(res.df)时，迭代将停止。默认的atol是相应dtype的最小正规数，默认的rtol是相应dtype精度的平方根。

order整型，默认值：8

要使用的有限差分公式的（正整数）阶数。奇数将向上取整到下一个偶数。

initial_step浮点型类数组，默认值：0.5

有限差分导数近似的（绝对）初始步长。

step_factor浮点型，默认值：2.0

每次迭代中步长减小的因子；即，迭代1中的步长为initial_step/step_factor。如果step_factor < 1，则后续步长将大于初始步长；如果小于某个阈值的步长是不希望的（例如由于减法抵消误差），这可能很有用。

maxiter整型，默认值：10

算法执行的最大迭代次数。请参阅备注。

step_direction整型类数组

一个表示有限差分步长方向的数组（用于x位于函数域边界附近的情况）。必须可与x和所有args广播。当为0（默认）时，使用中心差分；当为负值（例如-1）时，步长为非正；当为正值（例如1）时，所有步长均为非负。

preserve_shape布尔型，默认值：False

在下文中，“f的参数”指的是数组xi和argsi中的任何数组。设shape为x和args所有元素的广播形状（这与传入f的xi和argsi在概念上是不同的）。

  • 当preserve_shape=False（默认）时，f必须接受任意可广播形状的参数。

  • 当preserve_shape=True时，f必须接受形状为shape或shape + (n,)的参数，其中(n,)是函数被评估的横坐标数量。

无论哪种情况，对于xi中的每个标量元素xi[j]，f返回的数组必须在相同索引处包含标量f(xi[j])。因此，输出的形状始终是输入xi的形状。

请参阅示例。

callback可调用对象，可选

一个可选的用户提供函数，在第一次迭代之前和每次迭代之后调用。以callback(res)形式调用，其中res是一个_RichResult，类似于scipy.differentiate.derivative返回的对象（但包含当前迭代中所有变量的值）。如果callback引发StopIteration，算法将立即终止，并且scipy.differentiate.derivative将返回一个结果。callback不得修改res或其属性。

返回：
res_RichResult

一个类似于scipy.optimize.OptimizeResult实例的对象，具有以下属性。描述是假设值为标量；但是，如果f返回一个数组，则输出将是相同形状的数组。

success布尔型数组

算法成功终止（状态码0）时为True；否则为False。

status整型数组

表示算法退出状态的整数。

  • 0 : 算法收敛到指定的容差。

  • -1 : 误差估计增加，因此迭代被终止。

  • -2 : 达到最大迭代次数。

  • -3 : 遇到非有限值。

  • -4 : 迭代被callback终止。

  • 1 : 算法正常进行（仅在callback中）。

df浮点型数组

如果算法成功终止，则为f在x处的导数。

error浮点型数组

误差估计：当前导数估计与上一次迭代估计之间差值的幅度。

nit整型数组

算法执行的迭代次数。

nfev整型数组

f被评估的点数。

x浮点型数组

评估f导数的值（与args和step_direction广播后）。

另请参阅

jacobian, hessian

备注

该实现受jacobi [1]、numdifftools [2]和DERIVEST [3]的启发，但其实现更直接地（可以说有些天真地）遵循泰勒级数理论。在第一次迭代中，使用阶数为order、最大步长为initial_step的有限差分公式估算导数。随后的每次迭代中，最大步长会按step_factor减小，并重新估算导数，直到达到终止条件。误差估计是当前导数近似值与前一次迭代估计值之间差值的幅度。

有限差分公式的模板设计使得横坐标是“嵌套的”：在第一次迭代中，f在order + 1个点上被评估后，在随后的每次迭代中，f仅在两个新点上被评估；有限差分公式所需的order - 1个先前评估过的函数值被重用，而两个函数值（在距离x最远的点处的评估）则未使用。

步长是绝对的。当步长相对于x的幅值很小时，精度会丢失；例如，如果x是1e20，则默认初始步长0.5无法解析。因此，对于较大的x幅值，请考虑使用更大的初始步长。

在真实导数恰好为零的点上，默认容差难以满足。如果导数可能恰好为零，请考虑指定一个绝对容差（例如atol=1e-12）以改善收敛。

参考文献

[1]

Hans Dembinski (@HDembinski). jacobi. HDembinski/jacobi

[2]

Per A. Brodtkorb 和 John D’Errico. numdifftools. https://numdifftools.readthedocs.io/en/latest/

示例

计算np.exp在多个点x处的导数。

>>> import numpy as np
>>> from scipy.differentiate import derivative
>>> f = np.exp
>>> df = np.exp  # true derivative
>>> x = np.linspace(1, 2, 5)
>>> res = derivative(f, x)
>>> res.df  # approximation of the derivative
array([2.71828183, 3.49034296, 4.48168907, 5.75460268, 7.3890561 ])
>>> res.error  # estimate of the error
array([7.13740178e-12, 9.16600129e-12, 1.17594823e-11, 1.51061386e-11,
       1.94262384e-11])
>>> abs(res.df - df(x))  # true error
array([2.53130850e-14, 3.55271368e-14, 5.77315973e-14, 5.59552404e-14,
       6.92779167e-14])

显示随着步长减小，近似值的收敛情况。每次迭代中，步长会按step_factor减小，因此对于足够小的初始步长，每次迭代会将误差减小1/step_factor**order的因子，直到有限精度算术阻止进一步的改进。

>>> import matplotlib.pyplot as plt
>>> iter = list(range(1, 12))  # maximum iterations
>>> hfac = 2  # step size reduction per iteration
>>> hdir = [-1, 0, 1]  # compare left-, central-, and right- steps
>>> order = 4  # order of differentiation formula
>>> x = 1
>>> ref = df(x)
>>> errors = []  # true error
>>> for i in iter:
...     res = derivative(f, x, maxiter=i, step_factor=hfac,
...                      step_direction=hdir, order=order,
...                      # prevent early termination
...                      tolerances=dict(atol=0, rtol=0))
...     errors.append(abs(res.df - ref))
>>> errors = np.array(errors)
>>> plt.semilogy(iter, errors[:, 0], label='left differences')
>>> plt.semilogy(iter, errors[:, 1], label='central differences')
>>> plt.semilogy(iter, errors[:, 2], label='right differences')
>>> plt.xlabel('iteration')
>>> plt.ylabel('error')
>>> plt.legend()
>>> plt.show()
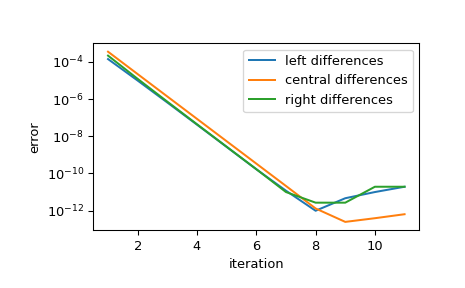
../../_images/scipy-differentiate-derivative-1_00_00.png 
>>> (errors[1, 1] / errors[0, 1], 1 / hfac**order)
(0.06215223140159822, 0.0625)

该实现对x、step_direction和args进行了向量化。函数在第一次迭代之前评估一次以执行输入验证和标准化，之后每次迭代评估一次。

>>> def f(x, p):
...     f.nit += 1
...     return x**p
>>> f.nit = 0
>>> def df(x, p):
...     return p*x**(p-1)
>>> x = np.arange(1, 5)
>>> p = np.arange(1, 6).reshape((-1, 1))
>>> hdir = np.arange(-1, 2).reshape((-1, 1, 1))
>>> res = derivative(f, x, args=(p,), step_direction=hdir, maxiter=1)
>>> np.allclose(res.df, df(x, p))
True
>>> res.df.shape
(3, 5, 4)
>>> f.nit
2

默认情况下，preserve_shape为False，因此可调用对象f可以以任意可广播形状的数组进行调用。例如

>>> shapes = []
>>> def f(x, c):
...    shape = np.broadcast_shapes(x.shape, c.shape)
...    shapes.append(shape)
...    return np.sin(c*x)
>>>
>>> c = [1, 5, 10, 20]
>>> res = derivative(f, 0, args=(c,))
>>> shapes
[(4,), (4, 8), (4, 2), (3, 2), (2, 2), (1, 2)]

为了理解这些形状的来源——并更好地理解derivative如何计算准确结果——请注意，c值越高对应着更高频率的正弦曲线。更高频率的正弦曲线使得函数的导数变化更快，因此需要更多的函数评估才能达到目标精度

>>> res.nfev
array([11, 13, 15, 17], dtype=int32)

初始的shape，(4,)，对应于在单个横坐标和所有四个频率下评估函数；这用于输入验证并确定存储结果的数组的大小和dtype。下一个形状对应于在初始横坐标网格和所有四个频率下评估函数。对函数的连续调用会在另外两个横坐标处评估函数，将近似的有效阶数提高两阶。然而，在后续的函数评估中，函数会在更少的频率下评估，因为相应的导数已经收敛到所需的容差。这可以节省函数评估以提高性能，但它要求函数接受任何形状的参数。

“向量值”函数不太可能满足此要求。例如，考虑

>>> def f(x):
...    return [x, np.sin(3*x), x+np.sin(10*x), np.sin(20*x)*(x-1)**2]

这个被积函数与当前形式的derivative不兼容；例如，输出的形状将与x的形状不同。这样的函数可以通过引入额外参数转换为兼容的形式，但这会很不方便。在这种情况下，一个更简单的解决方案是使用preserve_shape。

>>> shapes = []
>>> def f(x):
...     shapes.append(x.shape)
...     x0, x1, x2, x3 = x
...     return [x0, np.sin(3*x1), x2+np.sin(10*x2), np.sin(20*x3)*(x3-1)**2]
>>>
>>> x = np.zeros(4)
>>> res = derivative(f, x, preserve_shape=True)
>>> shapes
[(4,), (4, 8), (4, 2), (4, 2), (4, 2), (4, 2)]

此处，x的形状为(4,)。当preserve_shape=True时，函数可以用形状为(4,)或(4, n)的参数x调用，这就是我们观察到的现象。

本页目录