kmeans2#
- scipy.cluster.vq.kmeans2(data, k, iter=10, thresh=1e-05, minit='random', missing='warn', check_finite=True, *, rng=None)[source]#
使用 k-均值算法将一组观测值分类为 k 个簇。
该算法试图最小化观测值和质心之间的欧几里得距离。包括几种初始化方法。
- 参数:
- datandarray
一个“M”x“N”数组,包含“N”维中的“M”个观测值,或一个长度为“M”的数组,包含“M”个一维观测值。
- kint or ndarray
要形成的簇的数量以及要生成的质心的数量。如果 minit 初始化字符串是“matrix”,或者如果给出了 ndarray,则将其解释为要使用的初始簇。
- iterint, optional
k-均值算法运行的迭代次数。请注意,这与 kmeans 函数的 iters 参数的含义不同。
- threshfloat, optional
(尚未被使用)
- minitstr, optional
初始化方法。可用方法有“random”、“points”、“++”和“matrix”
“random”:从具有从数据估计的均值和方差的高斯分布中生成 k 个质心。
“points”:从数据中随机选择 k 个观测值(行)作为初始质心。
“++”:根据 kmeans++ 方法(小心播种)选择 k 个观测值
“matrix”:将 k 参数解释为 k x M(或一维数据的长度为 k 的数组)的初始质心数组。
- missingstr, optional
处理空簇的方法。可用方法有“warn”和“raise”
“warn”:发出警告并继续。
“raise”:引发 ClusterError 并终止算法。
- check_finitebool, optional
是否检查输入矩阵是否仅包含有限数字。禁用此选项可能会提高性能,但如果输入确实包含无穷大或 NaN,则可能会导致问题(崩溃、非终止)。默认值:True
- rng{None, int,
numpy.random.Generator}, optional 如果 rng 通过关键字传递,则
numpy.random.Generator之外的类型将传递给numpy.random.default_rng以实例化一个Generator。如果 rng 已经是一个Generator实例,则使用提供的实例。指定 rng 以获得可重复的函数行为。如果此参数通过位置传递或 seed 通过关键字传递,则参数 seed 应用旧行为
如果 seed 为 None(或
numpy.random),则使用numpy.random.RandomState单例。如果 seed 是一个整数,则使用一个新的
RandomState实例,并使用 seed 进行播种。如果 seed 已经是一个
Generator或RandomState实例,则使用该实例。
在版本 1.15.0 中更改:作为从使用
numpy.random.RandomState转换到numpy.random.Generator的 SPEC-007 过渡的一部分,此关键字已从 seed 更改为 rng。在过渡期间,这两个关键字将继续工作,但一次只能指定一个。在过渡期结束后,使用 seed 关键字的函数调用将发出警告。上面概述了 seed 和 rng 的行为,但在新代码中应仅使用 rng 关键字。
- 返回值:
- centroidndarray
在 k-均值的最后一次迭代中找到的质心的“k”x“N”数组。
- labelndarray
label[i] 是第 i 个观测值最接近的质心的代码或索引。
参见
备注
kmeans2除了 NumPy 之外,还实验性地支持 Python Array API Standard 兼容后端。 请考虑通过设置环境变量SCIPY_ARRAY_API=1并提供 CuPy、PyTorch、JAX 或 Dask 数组作为数组参数来测试这些功能。 支持以下后端和设备(或其他功能)的组合。库
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
✅
⛔
JAX
⚠️ 没有 JIT
⛔
Dask
⚠️ 计算图
n/a
有关更多信息,请参见 对数组 API 标准的支持。
参考文献
[1]D. Arthur and S. Vassilvitskii, “k-means++: the advantages of careful seeding”, Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2007.
示例
>>> from scipy.cluster.vq import kmeans2 >>> import matplotlib.pyplot as plt >>> import numpy as np
创建 z,一个形状为 (100, 2) 的数组,包含来自三个多元正态分布的样本混合。
>>> rng = np.random.default_rng() >>> a = rng.multivariate_normal([0, 6], [[2, 1], [1, 1.5]], size=45) >>> b = rng.multivariate_normal([2, 0], [[1, -1], [-1, 3]], size=30) >>> c = rng.multivariate_normal([6, 4], [[5, 0], [0, 1.2]], size=25) >>> z = np.concatenate((a, b, c)) >>> rng.shuffle(z)
计算三个簇。
>>> centroid, label = kmeans2(z, 3, minit='points') >>> centroid array([[ 2.22274463, -0.61666946], # may vary [ 0.54069047, 5.86541444], [ 6.73846769, 4.01991898]])
每个簇中有多少个点?
>>> counts = np.bincount(label) >>> counts array([29, 51, 20]) # may vary
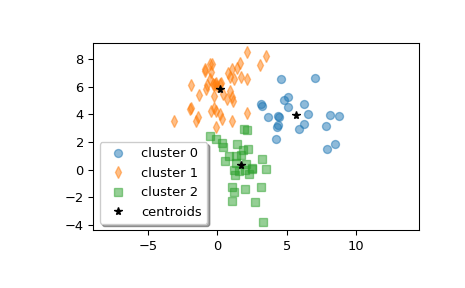
绘制簇。
>>> w0 = z[label == 0] >>> w1 = z[label == 1] >>> w2 = z[label == 2] >>> plt.plot(w0[:, 0], w0[:, 1], 'o', alpha=0.5, label='cluster 0') >>> plt.plot(w1[:, 0], w1[:, 1], 'd', alpha=0.5, label='cluster 1') >>> plt.plot(w2[:, 0], w2[:, 1], 's', alpha=0.5, label='cluster 2') >>> plt.plot(centroid[:, 0], centroid[:, 1], 'k*', label='centroids') >>> plt.axis('equal') >>> plt.legend(shadow=True) >>> plt.show()