scipy.cluster.hierarchy.

linkage

scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)

执行层次/凝聚聚类。

输入 y 可以是 1-D 压缩距离矩阵或 2-D 观测向量数组。

如果 y 是 1-D 压缩距离矩阵，那么 y 必须是一个大小为 \(\binom{n}{2}\) 的向量，其中 n 是距离矩阵中配对的原始观测的数量。 此函数的行为与 MATLAB linkage 函数非常相似。

返回一个 \((n-1)\) 行 4 列的矩阵 Z。 在第 \(i\) 次迭代中，索引为 Z[i, 0] 和 Z[i, 1] 的簇被组合以形成簇 \(n + i\)。 索引小于 \(n\) 的簇对应于 \(n\) 个原始观测值之一。 簇 Z[i, 0] 和 Z[i, 1] 之间的距离由 Z[i, 2] 给出。 第四个值 Z[i, 3] 表示新形成的簇中原始观测的数量。

以下链接方法用于计算两个簇 \(s\) 和 \(t\) 之间的距离 \(d(s, t)\)。 该算法从一个尚未在形成的层次结构中使用的簇的森林开始。 当森林中的两个簇 \(s\) 和 \(t\) 合并成一个簇 \(u\) 时，\(s\) 和 \(t\) 从森林中移除，并将 \(u\) 添加到森林中。 当森林中只剩下一个簇时，算法停止，这个簇成为根。

每次迭代都会维护一个距离矩阵。 d[i,j] 条目对应于原始森林中簇 \(i\) 和 \(j\) 之间的距离。

在每次迭代中，算法都必须更新距离矩阵，以反映新形成的簇 u 与森林中剩余簇的距离。

假设簇 \(u\) 中有 \(|u|\) 个原始观测值 \(u[0], \ldots, u[|u|-1]\)，簇 \(v\) 中有 \(|v|\) 个原始对象 \(v[0], \ldots, v[|v|-1]\)。 回想一下，\(s\) 和 \(t\) 被组合成簇 \(u\)。 设 \(v\) 为森林中不是 \(u\) 的任何剩余簇。

以下是计算新形成的簇 \(u\) 和每个 \(v\) 之间距离的方法。

• method='single' 指定

  \[d(u,v) = \min(dist(u[i],v[j]))\]

  对于簇 \(u\) 中的所有点 \(i\) 和簇 \(v\) 中的所有点 \(j\)。 这也称为最近点算法。

• method='complete' 指定

  \[d(u, v) = \max(dist(u[i],v[j]))\]

  对于簇 u 中的所有点 \(i\) 和簇 \(v\) 中的所有点 \(j\)。 这也称为最远点算法或 Voor Hees 算法。

• method='average' 指定

  \[d(u,v) = \sum_{ij} \frac{d(u[i], v[j])} {(|u|*|v|)}\]

  对于所有点 \(i\) 和 \(j\)，其中 \(|u|\) 和 \(|v|\) 分别是簇 \(u\) 和 \(v\) 的基数。 这也称为 UPGMA 算法。

• method='weighted' 指定

  \[d(u,v) = (dist(s,v) + dist(t,v))/2\]

  其中簇 u 是由簇 s 和 t 形成的，v 是森林中的剩余簇（也称为 WPGMA）。

• method='centroid' 指定

  \[dist(s,t) = ||c_s-c_t||_2\]

  其中 \(c_s\) 和 \(c_t\) 分别是簇 \(s\) 和 \(t\) 的质心。 当两个簇 \(s\) 和 \(t\) 合并成一个新簇 \(u\) 时，新的质心是在簇 \(s\) 和 \(t\) 中的所有原始对象上计算的。 然后，距离变为 \(u\) 的质心与森林中剩余簇 \(v\) 的质心之间的欧几里德距离。 这也称为 UPGMC 算法。

• method='median' 指定 \(d(s,t)\)，如 centroid 方法。 当两个簇 \(s\) 和 \(t\) 合并成一个新簇 \(u\) 时，质心 s 和 t 的平均值给出新的质心 \(u\)。 这也称为 WPGMC 算法。

• method='ward' 使用 Ward 方差最小化算法。 新的条目 \(d(u,v)\) 计算如下，

  \[d(u,v) = \sqrt{\frac{|v|+|s|} {T}d(v,s)^2 + \frac{|v|+|t|} {T}d(v,t)^2 - \frac{|v|} {T}d(s,t)^2}\]

  其中 \(u\) 是由簇 \(s\) 和 \(t\) 组成的新连接的簇，\(v\) 是森林中未使用的簇，\(T=|v|+|s|+|t|\)，并且 \(|*|\) 是其参数的基数。 这也称为增量算法。

警告：当选择森林中最小距离对时，可能存在两个或多个具有相同最小距离的对。 此实现可能会选择与 MATLAB 版本不同的最小值。

参数:

yndarray

压缩距离矩阵。 压缩距离矩阵是一个包含距离矩阵上三角的扁平数组。 这是 pdist 返回的形式。 或者，可以将 \(m\) 个观测向量的集合以 \(m\) 行 \(n\) 列的数组传递，其中 \(n\) 是维度。 压缩距离矩阵的所有元素都必须是有限的，即没有 NaN 或 inf。

methodstr, optional

要使用的链接算法。 有关完整说明，请参见下面的 链接方法 部分。

metricstr or function, optional

在 y 是观测向量集合的情况下要使用的距离度量； 否则将被忽略。 有关有效距离度量的列表，请参见 pdist 函数。 也可以使用自定义距离函数。

optimal_orderingbool, optional

如果为 True，则将重新排序链接矩阵，以便连续叶子之间的距离最小。 当数据可视化时，这会导致更直观的树结构。 默认为 False，因为此算法可能很慢，尤其是在大型数据集上 [2]。 另请参见 optimal_leaf_ordering 函数。

在版本 1.0.0 中添加。

返回值:

Zndarray

层次聚类被编码为链接矩阵。

另请参见

scipy.spatial.distance.pdist

成对距离度量

备注

1. 对于方法“single”，实现了基于最小生成树的优化算法。 它的时间复杂度为 \(O(n^2)\)。 对于方法“complete”、“average”、“weighted”和“ward”，实现了称为最近邻链的算法。 它的时间复杂度也为 \(O(n^2)\)。 对于其他方法，实现了一种朴素算法，其时间复杂度为 \(O(n^3)\)。 所有算法都使用 \(O(n^2)\) 内存。 有关算法的详细信息，请参阅 [1]。

2. 只有在使用欧几里德成对度量时，才能正确定义方法“centroid”、“median”和“ward”。 如果 y 作为预先计算的成对距离传递，那么用户有责任确保这些距离实际上是欧几里德距离，否则产生的结果将不正确。

linkage 除了 NumPy 之外，还对 Python Array API Standard 兼容后端提供实验性支持。 请考虑通过设置环境变量 SCIPY_ARRAY_API=1 并提供 CuPy、PyTorch、JAX 或 Dask 数组作为数组参数来测试这些功能。 支持以下后端和设备（或其他功能）的组合。

库	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	⛔
PyTorch	✅	⛔
JAX	✅	⛔
Dask	⚠️ 合并块	n/a

有关更多信息，请参见 对数组 API 标准的支持。

参考

[1]

Daniel Mullner，“现代层次，凝聚聚类算法”，arXiv:1109.2378v1。

[2]

Ziv Bar-Joseph、David K. Gifford、Tommi S. Jaakkola，“层次聚类的快速最优叶排序”，2001 年。生物信息学 DOI:10.1093/bioinformatics/17.suppl_1.S22

示例

在浏览器中尝试一下！

>>> from scipy.cluster.hierarchy import dendrogram, linkage
>>> from matplotlib import pyplot as plt
>>> X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]

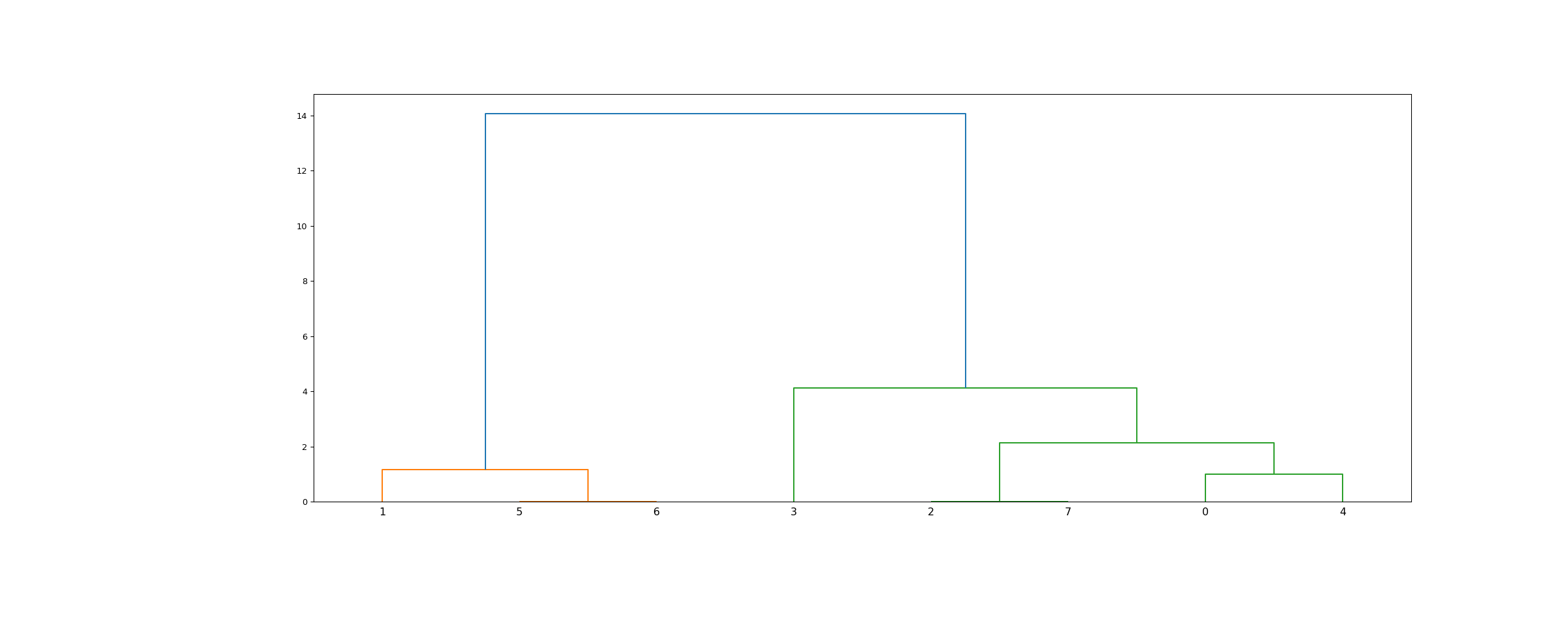
>>> Z = linkage(X, 'ward')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)

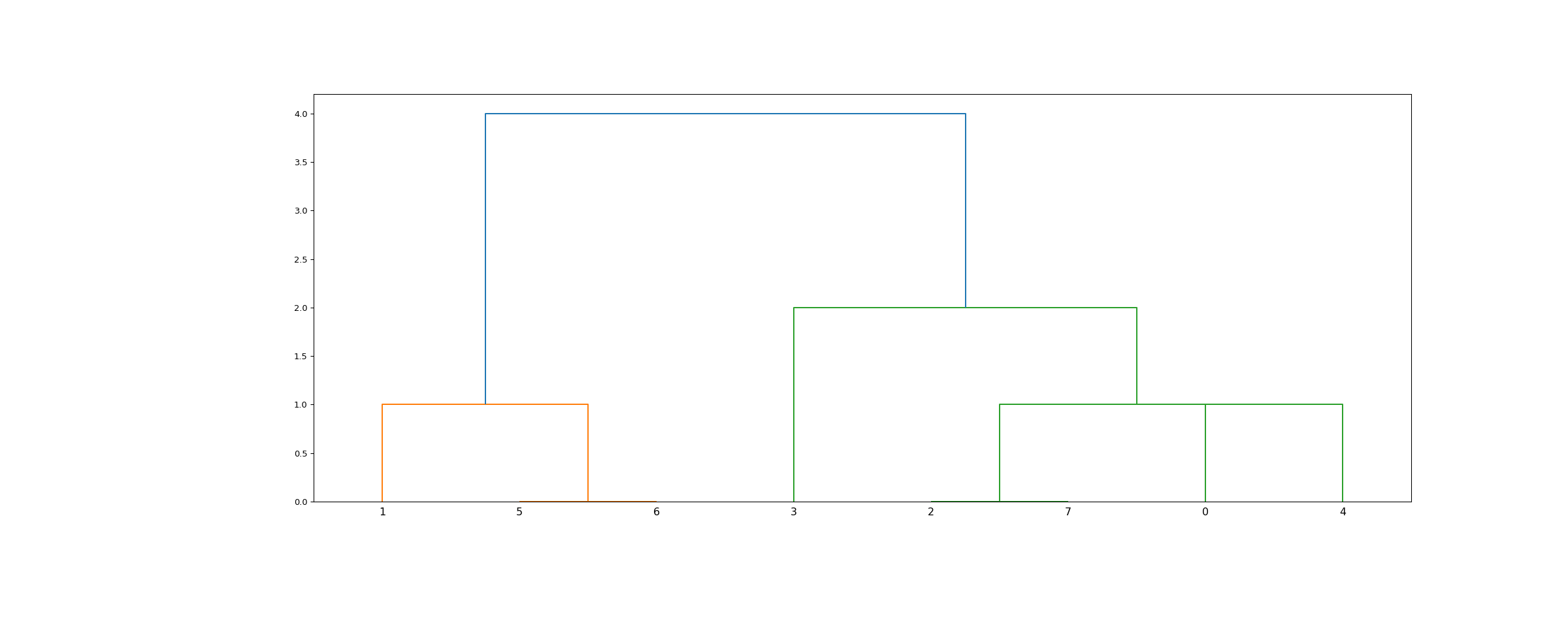
>>> Z = linkage(X, 'single')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)
>>> plt.show()

返回在新标签页中打开