基于多项式插值的累积分布函数逆变换（PINV）

• 必需：PDF

• 可选：CDF，众数，中心

• 速度

  • 设置：（非常）慢

  • 采样：（非常）快

基于多项式插值的累积分布函数逆变换（PINV）是一种仅需密度函数即可从分布中采样得到的反演方法。它基于 PPF 的多项式插值和 PDF 的高斯-洛巴托积分。它可以控制插值误差和积分误差。其主要目的是提供非常快的采样，对于任何给定的分布，其采样速度几乎相同，但代价是设置时间中等或较慢。它是已知固定参数情况下最快的反演方法。

反演方法是最简单且最灵活的采样非均匀随机变量的方法。对于具有 CDF \(F\) 的目标分布和从 \(\text{Uniform}(0, 1)\) 采样的均匀随机变量 \(U\)，通过使用分布的 PPF（逆 CDF）转换均匀随机变量 \(U\) 生成随机变量 X

\[X = F^{-1}(U)\]

由于其优点，此方法适用于随机模拟。其中一些最吸引人的优点是

• 它保留了均匀随机数采样器的结构属性。

• 将均匀随机变量 \(U\) 一对一转换为非均匀随机变量 \(X\)。

• 易于且有效地从截断分布中采样。

不幸的是，PPF 很少以封闭形式可用，或者可用时速度太慢。对于许多分布，CDF 也不容易获得。此方法解决了这两个缺点。用户只需提供 PDF，以及可选的众数附近的点（称为“中心”）以及最大可接受误差的大小。它使用自适应和简单高斯-洛巴托求积的组合来获得 CDF，并使用牛顿插值法来获得 PPF。该方法不是精确的，因为它仅产生近似分布的随机变量。尽管如此，最大容许的近似误差可以设置为接近机器精度。u 误差的概念用于测量和控制误差。它定义为

\[\epsilon_{u}(u) = | u - F\left(F^{-1}_{a}(u)\right) |\]

其中 \(u \in (0, 1)\) 是我们要测量误差的分位数，而 \(F^{-1}_a\) 是给定分布的近似 PPF。

最大 u 误差是数值计算 CDF 和 PPF 时近似误差的标准。算法的最大容许 u 误差称为算法的 u 分辨率，用 \(\epsilon_{u}\) 表示

\[\sup_{u \in (0,1)} | u - F\left(F^{-1}_{a}(u)\right) | \le \epsilon_{u}\]

u 误差的主要优点是，如果 CDF 可用，则可以轻松计算 u 误差。有关更详细的讨论，请参阅 [1]。

此外，该方法仅适用于有界分布。对于无限尾部的情况，尾部的末端将被截断，使得它们之下的面积小于或等于 \(0.05\epsilon_{u}\)。

对于给定的分布，有一些限制

• 分布的支撑（即 PDF 严格为正的区域）必须是连通的。实际上，这意味着 PDF“不太小”的区域必须是连通的。单峰密度满足此条件。如果违反此条件，则可能会截断分布的域。

• 当 PDF 以数值方式积分时，给定的 PDF 必须是连续的并且应该是平滑的。

• PDF 必须是有界的。

• 当分布具有重尾（因为逆 CDF 在 0 或 1 处变得非常陡峭）并且请求的 u 分辨率非常小时，该算法会出现问题。例如，当请求的 u 分辨率小于 1e-12 时，柯西分布很可能出现此问题。

算法在设置期间执行以下四个步骤

• 计算分布的端点：如果给定有限支撑，则跳过此步骤。否则，尾部的末端将被截断，使得它们之下的面积小于或等于 \(0.05\epsilon_{u}\)。

• 将域划分为子区间以计算 CDF 和 PPF。

• 使用高斯-洛巴托求积计算 CDF，使得积分误差最多为 \(0.05I_{0}\epsilon_{u}\)，其中 \(I_{0}\) 近似为 PDF 下的总面积。

• 使用牛顿插值公式计算 PPF，最大插值误差为 \(0.9\epsilon_{u}\)。

要初始化生成器以从标准正态分布中采样，请执行以下操作

>>> import numpy as np
>>> from scipy.stats.sampling import NumericalInversePolynomial
>>> class StandardNormal:
...     def pdf(self, x):
...         return np.exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)

生成器已设置好，我们可以开始从我们的分布中采样

>>> rng.rvs((5, 3))
array([[-1.52449963,  1.31933688,  2.05884468],
       [ 0.48883931,  0.15207903, -0.02150773],
       [ 1.11486463,  1.95449597, -0.30724928],
       [ 0.9854643 ,  0.29867424,  0.7560304 ],
       [-0.61776203,  0.16033378, -1.00933003]])

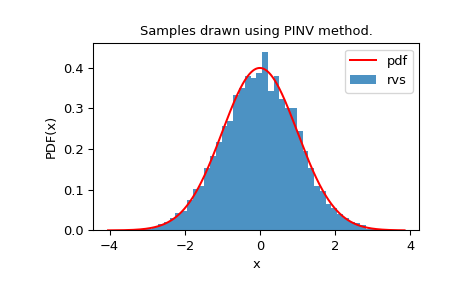
我们可以查看随机变量的直方图，以检查它们与我们的分布的拟合程度

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import norm
>>> from scipy.stats.sampling import NumericalInversePolynomial
>>> class StandardNormal:
...     def pdf(self, x):
...         return np.exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, num=10000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, "r-", label="pdf")
>>> plt.hist(rvs, bins=50, density=True, alpha=0.8, label="rvs")
>>> plt.xlabel("x")
>>> plt.ylabel("PDF(x)")
>>> plt.title("Samples drawn using PINV method.")
>>> plt.legend()
>>> plt.show()

可以通过在初始化期间传递 u_resolution 关键字来更改最大容许误差（即 u 分辨率）

>>> rng = NumericalInversePolynomial(dist, u_resolution=1e-12,
...                                  random_state=urng)

这会导致 PPF 的更精确的近似，并且生成的 RV 更密切地遵循精确的分布。尽管如此，请注意，它需要付出昂贵的设置代价。

设置时间主要取决于 PDF 的评估次数。对于难以评估的 PDF，成本更高。请注意，我们可以忽略归一化常数，以加快 PDF 的评估速度。在 u_resolution 值较小时，设置期间的 PDF 评估次数会增加。

>>> from scipy.stats.sampling import NumericalInversePolynomial
>>> class StandardNormal:
...     def __init__(self):
...         self.callbacks = 0
...     def pdf(self, x):
...         self.callbacks += 1
...         return np.exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> # u_resolution = 10^-8
>>> # => less PDF evaluations required
>>> # => faster setup
>>> rng = NumericalInversePolynomial(dist, u_resolution=1e-8,
...                                  random_state=urng)
>>> dist.callbacks
4095        # may vary
>>> dist.callbacks = 0  # reset the number of callbacks
>>> # u_resolution = 10^-10 (default)
>>> # => more PDF evaluations required
>>> # => slow setup
>>> rng = NumericalInversePolynomial(dist, u_resolution=1e-10,
...                                  random_state=urng)
>>> dist.callbacks
11454       # may vary
>>> dist.callbacks = 0  # reset the number of callbacks
>>> # u_resolution = 10^-12
>>> # => lots of PDF evaluations required
>>> # => very slow setup
>>> rng = NumericalInversePolynomial(dist, u_resolution=1e-12,
...                                  random_state=urng)
13902     # may vary

正如我们所看到的，所需的 PDF 评估次数非常高，快速 PDF 对于算法至关重要。但是，这有助于减少实现误差目标所需的子区间数量，从而节省内存并使采样速度更快。NumericalInverseHermite 是一种类似的反演方法，它基于埃尔米特插值反演 CDF，并通过 u 分辨率控制最大容许误差。但是，与 NumericalInversePolynomial 相比，它使用了更多的区间

>>> from scipy.stats.sampling import NumericalInverseHermite
>>> # NumericalInverseHermite accepts a `tol` parameter to set the
>>> # u-resolution of the generator.
>>> rng_hermite = NumericalInverseHermite(norm(), tol=1e-12)
>>> rng_hermite.intervals
3000
>>> rng_poly = NumericalInversePolynomial(norm(), u_resolution=1e-12)
>>> rng_poly.intervals
252

当分布的精确 CDF 可用时，可以通过调用 u_error 方法来估计算法实现的 u 误差

>>> from scipy.special import ndtr
>>> class StandardNormal:
...     def pdf(self, x):
...         return np.exp(-0.5 * x*x)
...     def cdf(self, x):
...         return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)
>>> rng.u_error(sample_size=100_000)
UError(max_error=8.785949745515609e-11, mean_absolute_error=2.9307548109436816e-11)

u_error 运行蒙特卡罗模拟，其中包含给定数量的样本来估计 u 误差。在上面的示例中，模拟使用 100,000 个样本来近似 u 误差。它以 UError 命名元组形式返回最大 u 误差（max_error）和平均绝对 u 误差（mean_absolute_error）。正如我们所看到的，max_error 低于默认的 u_resolution（1e-10）。

初始化生成器后，还可以评估给定分布的 PPF

>>> rng.ppf(0.975)
1.959963985701268
>>> norm.ppf(0.975)
1.959963984540054

例如，我们可以使用它来检查最大和平均绝对 u 误差

>>> u = np.linspace(0.001, 0.999, num=1_000_000)
>>> u_errors = np.abs(u - dist.cdf(rng.ppf(u)))
>>> u_errors.max()
8.78600525666684e-11
>>> u_errors.mean()
2.9321444940323206e-11

生成器提供的近似 PPF 方法比分布的精确 PPF 计算速度快得多。

在设置过程中，会存储一个 CDF 点表，一旦生成器被创建，就可以使用该表来近似 CDF。

>>> rng.cdf(1.959963984540054)
0.9750000000042454
>>> norm.cdf(1.959963984540054)
0.975

我们可以使用它来检查计算 CDF 时的积分误差是否超过 \(0.05I_{0}\epsilon_{u}\)。这里 \(I_0\) 是 \(\sqrt{2\pi}\) （标准正态分布的归一化常数）。

>>> x = np.linspace(-10, 10, num=100_000)
>>> x_error = np.abs(dist.cdf(x) - rng.cdf(x))
>>> x_error.max()
4.506062190046123e-12
>>> I0 = np.sqrt(2*np.pi)
>>> max_integration_error = 0.05 * I0 * 1e-10
>>> x_error.max() <= max_integration_error
True

设置期间计算的 CDF 表用于评估 CDF，只需要进行一些进一步的微调。这减少了对 PDF 的调用次数，但是由于微调步骤使用了简单的 Gauss-Lobatto 正交，PDF 会被调用多次，从而减慢了计算速度。

参考文献

[1]

Derflinger, Gerhard, Wolfgang Hörmann, 和 Josef Leydold. “Random variate generation by numerical inversion when only the density is known.” ACM Transactions on Modeling and Computer Simulation (TOMACS) 20.4 (2010): 1-25.