scipy.signal.

cwt#

scipy.signal.cwt(data, wavelet, widths, dtype=None, **kwargs)[source]#

连续小波变换。

从 1.12.0 版本开始弃用：scipy.signal.cwt 在 SciPy 1.12 中弃用，将在 SciPy 1.15 中移除。我们建议改用 PyWavelets。

利用小波函数对 data 执行连续小波变换。CWT 使用小波函数对 data 进行卷积，其特征在于宽度参数和长度参数。允许小波函数呈复杂的。

参数：

data(N,) ndarray: 执行变换的数据。
wavelet函数: 小波函数，应采用 2 个参数。第一个参数是要返回的矢量的点数（len(wavelet(length, width)) == length）。第二个参数是宽度参数，定义小波的大小（例如，高斯分布的标准偏差）。请参见 ricker，它满足这些要求。
widths(M,) sequence: 用于变换的宽度。
dtype数据类型，可选: 输出的期望数据类型。如果 wavelet 的输出是实数，则默认为 float64，如果是复数则默认为 complex128。

已添加至 1.4.0 版。
kwargs: 传递给小波函数的关键字自变量。

已添加至 1.4.0 版。

返回:

cwt: (M, N) ndarray: 具有 (len(宽度), len(数据)) 的形状。

说明

已添加至 1.4.0 版。

对于非对称的复值小波，输入信号会与小波数据的时逆复共轭相卷积 [1]。

length = min(10 * width[ii], len(data))
cwt[ii,:] = signal.convolve(data, np.conj(wavelet(length, width[ii],
                                **kwargs))[::-1], mode='same')

参考资料

[1]

S. Mallat，“小波信号处理巡礼（第 3 版）”，Academic Press，2009 年。

示例

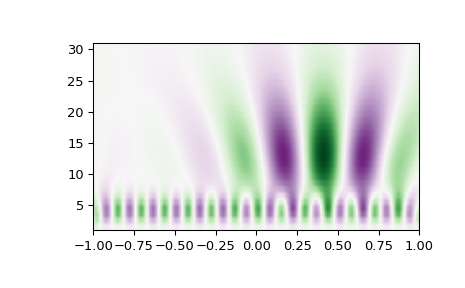
>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> t = np.linspace(-1, 1, 200, endpoint=False)
>>> sig  = np.cos(2 * np.pi * 7 * t) + signal.gausspulse(t - 0.4, fc=2)
>>> widths = np.arange(1, 31)
>>> cwtmatr = signal.cwt(sig, signal.ricker, widths)

注意

对于 cwt 矩阵绘图，建议反转 y 轴。

>>> cwtmatr_yflip = np.flipud(cwtmatr)
>>> plt.imshow(cwtmatr_yflip, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto',
...            vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max())
>>> plt.show()