正态性检验#
函数 scipy.stats.normaltest 检验样本是否来自正态分布的零假设。它基于 D'Agostino 和 Pearson 的[1] [2] 检验,该检验结合偏度和峰度来产生一个正态性的综合检验。
假设我们希望从测量结果中推断,在一项医学研究中,成年男性体重是否不呈正态分布[3]。体重(磅)记录在下面的数组 x 中。
import numpy as np
x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])
[1] 和 [2] 中的正态性检验 scipy.stats.normaltest 首先计算一个基于样本偏度和峰度的统计量。
from scipy import stats
res = stats.normaltest(x)
res.statistic
np.float64(13.034263121192582)
(该测试警告我们的样本观察值太少,无法执行测试。我们将在示例末尾再次讨论这一点。)由于正态分布具有零偏度和零(“超额”或“Fisher”)峰度,因此从正态分布中抽取的样本的该统计量值往往较低。
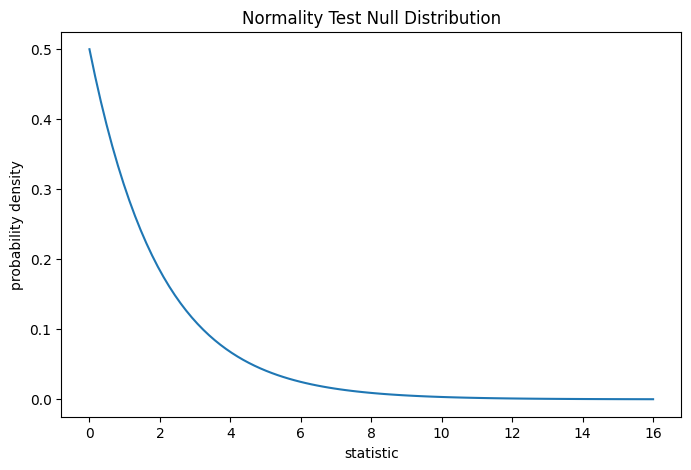
通过将统计量的观测值与零分布进行比较来执行该检验:零分布是在零假设(即体重是从正态分布中抽取的)下推导出的统计量值的分布。对于此正态性检验,对于非常大的样本,零分布是具有两个自由度的卡方分布。
import matplotlib.pyplot as plt
dist = stats.chi2(df=2)
stat_vals = np.linspace(0, 16, 100)
pdf = dist.pdf(stat_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(stat_vals, pdf)
ax.set_title("Normality Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
通过 p 值量化比较:零分布中大于或等于统计量观测值的比例。
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.6f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (13.5, 5e-4), (14, 5e-3), arrowprops=props)
i = stat_vals >= res.statistic # index more extreme statistic values
ax.fill_between(stat_vals[i], y1=0, y2=pdf[i])
ax.set_xlim(8, 16)
ax.set_ylim(0, 0.01)
plt.show()
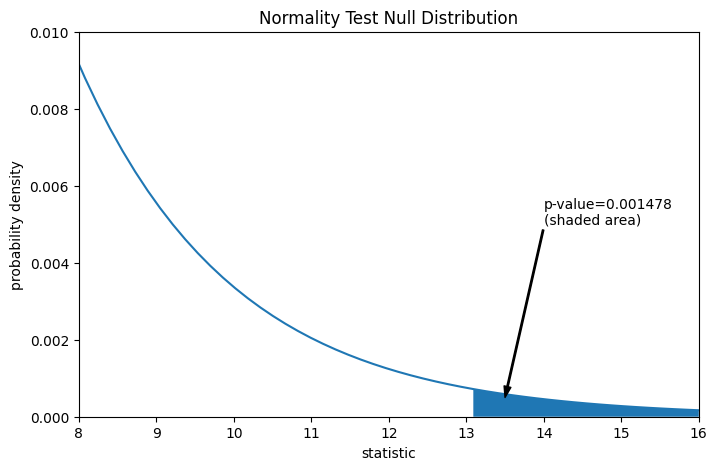
res.pvalue
np.float64(0.0014779023013100172)
如果 p 值“小”——也就是说,从正态分布的总体中抽取数据产生如此极端的统计量值的概率很低——这可以作为反对零假设的证据,转而支持备择假设:体重并非来自正态分布。请注意
反之则不成立;也就是说,该检验不用于提供支持零假设的证据。
对于将被视为“小”的值的阈值,应在分析数据之前做出选择[4],并考虑假阳性(错误地拒绝零假设)和假阴性(未能拒绝错误的零假设)的风险。
请注意,卡方分布提供了零分布的渐近近似;它只对有许多观测值的样本准确。这就是我们在示例开头收到警告的原因;我们的样本非常小。在这种情况下,scipy.stats.monte_carlo_test 可能会提供更准确(尽管是随机的)的精确 p 值近似。
def statistic(x, axis):
# Get only the `normaltest` statistic; ignore approximate p-value
return stats.normaltest(x, axis=axis).statistic
res = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
alternative='greater')
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
ax.hist(res.null_distribution, np.linspace(0, 25, 50),
density=True)
ax.legend(['asymptotic approximation (many observations)',
'Monte Carlo approximation (11 observations)'])
ax.set_xlim(0, 14)
plt.show()
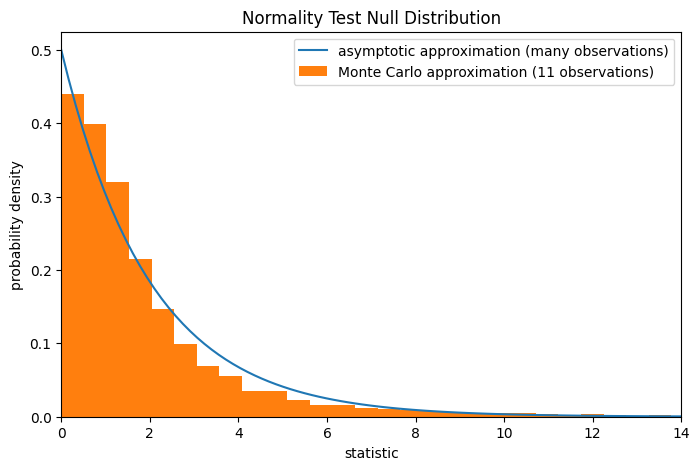
res.pvalue
np.float64(0.0075)
此外,尽管 p 值具有随机性,但以这种方式计算的 p 值可用于精确控制零假设的错误拒绝率[5]。