scipy.spatial.transform.

RigidTransform#

class scipy.spatial.transform.RigidTransform#

3 维刚性变换。

此类提供了一个接口，用于从 3D 空间中的刚性变换（旋转和平移）进行初始化和表示。在不同的领域，这种类型的变换可能被称为“姿势”（尤其是在机器人技术中）、“外部参数”或“模型矩阵”（尤其是在计算机图形学中），但核心概念是相同的：描述一个 3D 坐标系相对于另一个坐标系的旋转和平移。从数学上讲，这些变换属于特殊欧几里德群 SE(3)，它编码了旋转 (SO(3)) 加上平移。

支持对刚性变换执行以下操作

在向量上应用
变换组合
变换求逆
变换索引

请注意，坐标系必须是右手坐标系。因此，此类更精确地表示 SE(3) 中的真刚性变换，而不是更普遍的 E(3) 中的刚性变换 [1]。

由于多个变换可以存储在单个 RigidTransform 实例中，因此支持在变换内进行索引。

要创建 RigidTransform 对象，请使用 from_... 方法（参见下面的示例）。RigidTransform(...) 不应直接实例化。

有关刚性变换的严格介绍，请参见 [2]、[3] 和 [4]。

属性:

single: 此实例是否表示单个变换。
rotation: 返回变换的旋转分量。
translation: 返回变换的平移分量。

方法

`__len__`(self)	返回此对象中的变换数量。
`__getitem__`(self, indexer)	从此对象中提取给定索引处的变换。
`__mul__`(self, RigidTransform other)	将此变换与另一个变换组合。
`__pow__`(self, float n)	将此变换与自身组合 n 次。
`from_matrix`(cls, matrix)	从 4x4 变换矩阵初始化。
`from_rotation`(cls, rotation)	从旋转初始化，不带平移。
`from_translation`(cls, translation)	从平移 numpy 数组初始化，不带旋转。
`from_components`(cls, translation, rotation)	从平移和旋转分量初始化刚性变换。
`from_exp_coords`(cls, exp_coords)	从变换的指数坐标初始化。
`from_dual_quat`(cls, dual_quat, *[, scalar_first])	从单位对偶四元数初始化。
`as_matrix`(self)	返回变换的矩阵表示的副本。
`as_components`(self)	返回变换的平移和旋转分量，其中先应用旋转，然后再应用平移。
`as_exp_coords`(self)	返回变换的指数坐标。
`as_dual_quat`(self, *[, scalar_first])	返回变换的对偶四元数表示。
`concatenate`(cls, transforms)	将 `RigidTransform` 对象序列连接到单个对象中。
`apply`(self, vector[, inverse])	将变换应用于向量。
`inv`(self)	反转此变换。
`identity`(cls[, num])	初始化单位变换。

注释

在版本 1.16.0 中添加。

参考文献

[1]

https://en.wikipedia.org/wiki/Rigid_transformation

[2]

https://motion.cs.illinois.edu/RoboticSystems/CoordinateTransformations.html

[3]

https://www.brainvoyager.com/bv/doc/UsersGuide/CoordsAndTransforms/SpatialTransformationMatrices.html

[4]

Kevin M. Lynch 和 Frank C. Park，“现代机器人学：力学、规划和控制”第 3.3 章，2017 年，剑桥大学出版社。 https://hades.mech.northwestern.edu/images/2/25/MR-v2.pdf#page=107.31

[5]

Paul Furgale，“表示机器人姿势：好的、坏的和丑陋的”，2014 年 6 月 9 日。 https://rpg.ifi.uzh.ch/docs/teaching/2024/FurgaleTutorial.pdf

示例

RigidTransform 实例可以在上述任何格式中初始化，并转换为其他格式。底层对象独立于用于初始化的表示形式。

符号约定和组合

此处的符号在很大程度上遵循 [5] 中定义的约定。当我们命名变换时，我们从右到左读取下标。因此，tf_A_B 表示变换 A <- B，可以解释为

B 相对于 A 的坐标和方向
将点从 B 变换到 A
在 A 的坐标系中描述的 B 的姿势

tf_A_B
   ^ ^
   | |
   | --- from B
   |
   ----- to A

组合变换时，顺序很重要。变换不具有交换性，因此通常 tf_A_B * tf_B_C 与 tf_B_C * tf_A_B 不同。变换从右到左组合并应用于向量。因此，(tf_A_B * tf_B_C).apply(p_C) 与 tf_A_B.apply(tf_B_C.apply(p_C)) 相同。

组合变换时，变换的顺序应使乘法运算符被单个框架包围，因此框架“抵消”并且外部框架保持不变。在下面的示例中，B 抵消，外部框架 A 和 C 保持不变。或者换句话说，A <- C 与 A <- B <- C 相同。

              ----------- B cancels out
              |      |
              v      v
tf_A_C = tf_A_B * tf_B_C
            ^          ^
            |          |
            ------------ to A, from C are left

当我们注释向量时，我们写下向量定义的框架的下标。因此，p_B 表示在框架 B 中定义的点 p。要将此点从框架 B 变换到框架 A 中的坐标，我们将变换 tf_A_B 应用于向量，使带注释的 B 框架彼此相邻并“抵消”。

           ------------ B cancels out
           |         |
           v         v
p_A = tf_A_B.apply(p_B)
         ^
         |
         -------------- A is left

可视化

>>> from scipy.spatial.transform import RigidTransform as Tf
>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

以下函数可用于通过显示变换标准 x、y、z 坐标轴的方式来使用 Matplotlib 绘制变换

>>> import matplotlib.pyplot as plt
>>> colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
>>> def plot_transformed_axes(ax, tf, name=None, scale=1):
...     r = tf.rotation
...     t = tf.translation
...     loc = np.array([t, t])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + t
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*tf.translation, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

定义框架

让我们完成一个例子。

首先，定义“世界框架” A，也称为“基本框架”。从他们自己的角度来看，所有框架都是单位变换。

>>> tf_A = Tf.identity()

我们将在 A 的坐标系中可视化一个新的框架 B。因此，我们需要定义将坐标从框架 B 转换为框架 A 的变换（A <- B）。

从物理上讲，让我们想象一下通过以下方式从 A 构造 B

绕其 x 轴将 A 旋转 +90 度。
将旋转后的框架在 A 的 -x 方向上平移 2 个单位。

从 A 的角度来看，B 位于 [-2, 0, 0]，并绕 x 轴旋转 +90 度，这正是变换 A <- B。

>>> t_A_B = np.array([-2, 0, 0])
>>> r_A_B = R.from_euler('xyz', [90, 0, 0], degrees=True)
>>> tf_A_B = Tf.from_components(t_A_B, r_A_B)

让我们绘制这些框架。

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> ax.set_title("A, B frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

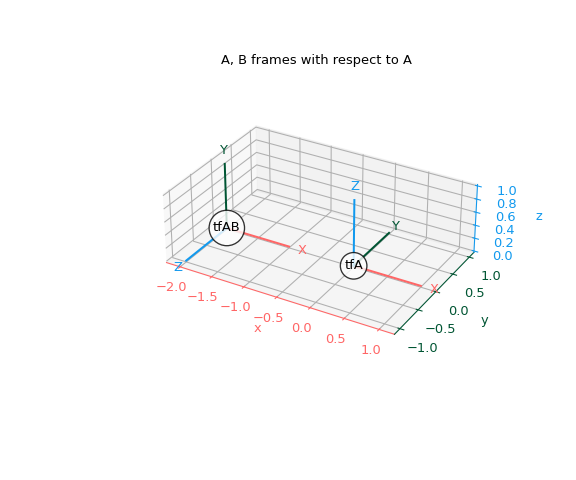
../../_images/scipy-spatial-transform-RigidTransform-1_00_00.png

现在让我们在 B 的坐标系中可视化一个新的框架 C。让我们想象一下通过以下方式从 B 构造 C

在其 +z 方向上将 B 平移 2 个单位。
绕其 z 轴将 B 旋转 +30 度。

>>> t_B_C = np.array([0, 0, 2])
>>> r_B_C = R.from_euler('xyz', [0, 0, 30], degrees=True)
>>> tf_B_C = Tf.from_components(t_B_C, r_B_C)

为了从一致的角度绘制这些框架，我们需要计算 A 和 C 之间的变换。请注意，我们不会直接进行此变换，而是组合中间变换，让我们从 C 到 A

>>> tf_A_C = tf_A_B * tf_B_C  # A <- B <- C

现在我们可以从 A 的角度绘制这三个框架。

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.set_title("A, B, C frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

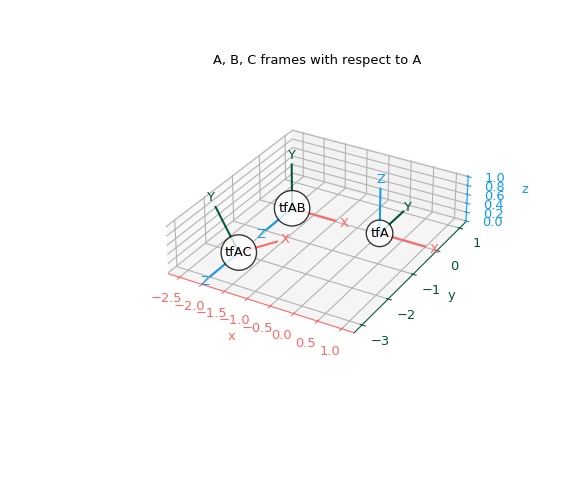
../../_images/scipy-spatial-transform-RigidTransform-1_01_00.png

变换向量

让我们将向量从 A 变换到 B 和 C。为此，我们将首先反转我们已经从 B 和 C 到 A 的变换。

>>> tf_B_A = tf_A_B.inv()  # B <- A
>>> tf_C_A = tf_A_C.inv()  # C <- A

现在我们可以定义 A 中的一个点，并使用上述变换来获得它在 B 和 C 中的坐标

>>> p1_A = np.array([1, 0, 0])  # +1 in x_A direction
>>> p1_B = tf_B_A.apply(p1_A)
>>> p1_C = tf_C_A.apply(p1_A)
>>> print(p1_A)  # Original point 1 in A
[1 0 0]
>>> print(p1_B)  # Point 1 in B
[3. 0. 0.]
>>> print(p1_C)  # Point 1 in C
[ 2.59807621 -1.5       -2.        ]

我们也可以反过来。我们定义 C 中的一个点并将其变换为 A

>>> p2_C = np.array([0, 1, 0])  # +1 in y_C direction
>>> p2_A = tf_A_C.apply(p2_C)
>>> print(p2_C)  # Original point 2 in C
[0 1 0]
>>> print(p2_A)  # Point 2 in A
[-2.5       -2.         0.8660254]

再次相对于 A 绘制框架，但也绘制这两个点

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.scatter(p1_A[0], p1_A[1], p1_A[2], color=colors[0])  # +1 x_A
>>> ax.scatter(p2_A[0], p2_A[1], p2_A[2], color=colors[1])  # +1 y_C
>>> ax.set_title("A, B, C frames and points with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

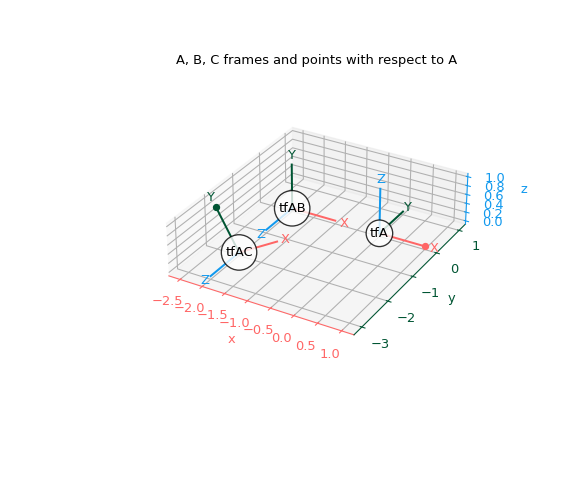
../../_images/scipy-spatial-transform-RigidTransform-1_02_00.png

切换基本框架

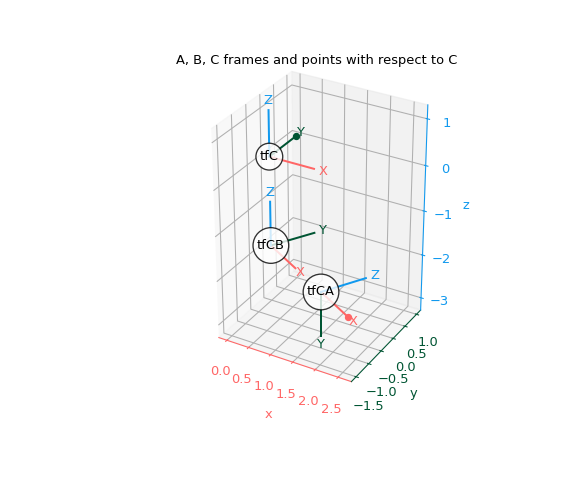
到目前为止，我们一直在从 A 的角度可视化框架。让我们使用我们定义的变换从 C 的角度可视化框架。

现在 C 是“基本框架”或“世界框架”。从他们自己的角度来看，所有框架都是单位变换。

>>> tf_C = Tf.identity()

我们已经定义了变换 C <- A，并且可以通过反转现有变换 B <- C 来获得 C <- B。

>>> tf_C_B = tf_B_C.inv()  # C <- B

这让我们从 C 的角度绘制所有内容

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_C, name="tfC")     # C plotted in C
>>> plot_transformed_axes(ax, tf_C_B, name="tfCB")  # B plotted in C
>>> plot_transformed_axes(ax, tf_C_A, name="tfCA")  # A plotted in C
>>> ax.scatter(p1_C[0], p1_C[1], p1_C[2], color=colors[0])
>>> ax.scatter(p2_C[0], p2_C[1], p2_C[2], color=colors[1])
>>> ax.set_title("A, B, C frames and points with respect to C")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

../../_images/scipy-spatial-transform-RigidTransform-1_03_00.png