空间数据结构和算法 (scipy.spatial)#
scipy.spatial 可以利用 Qhull 库计算一组点的三角剖分、Voronoi 图和凸包。
此外,它包含 KDTree 用于最近邻点查询的实现,以及用于各种度量中距离计算的实用程序。
德劳内三角剖分#
德劳内三角剖分是将一组点细分为一组不重叠的三角形,使得任何点都不在任何三角形的圆周内。在实践中,这种三角剖分往往避免了具有小角度的三角形。
可以使用 scipy.spatial 计算德劳内三角剖分,如下所示
>>> from scipy.spatial import Delaunay
>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> tri = Delaunay(points)
我们可以将其可视化
>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
并添加一些进一步的装饰
>>> for j, p in enumerate(points):
... plt.text(p[0]-0.03, p[1]+0.03, j, ha='right') # label the points
>>> for j, s in enumerate(tri.simplices):
... p = points[s].mean(axis=0)
... plt.text(p[0], p[1], '#%d' % j, ha='center') # label triangles
>>> plt.xlim(-0.5, 1.5); plt.ylim(-0.5, 1.5)
>>> plt.show()
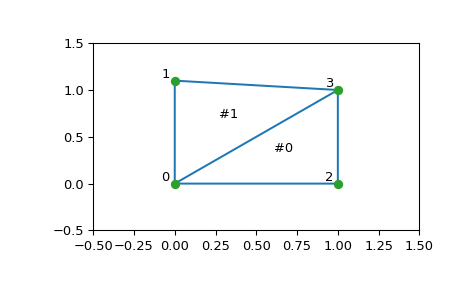
三角剖分的结构以以下方式编码:simplices 属性包含构成三角形的 points 数组中点的索引。例如
>>> i = 1
>>> tri.simplices[i,:]
array([3, 1, 0], dtype=int32)
>>> points[tri.simplices[i,:]]
array([[ 1. , 1. ],
[ 0. , 1.1],
[ 0. , 0. ]])
此外,还可以找到相邻三角形
>>> tri.neighbors[i]
array([-1, 0, -1], dtype=int32)
这告诉我们,这个三角形有一个邻居,即三角形 #0,但没有其他邻居。此外,它告诉我们邻居 0 与三角形的顶点 1 相反
>>> points[tri.simplices[i, 1]]
array([ 0. , 1.1])
事实上,从图中我们可以看到,情况确实如此。
Qhull 还可以对更高维度的点集执行单纯形细分(例如,在 3-D 中细分为四面体)。
共面点#
重要的是要注意,并非所有点都一定出现在三角剖分的顶点,这是由于形成三角剖分的数值精度问题。考虑上面带有重复点的示例
>>> points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
>>> tri = Delaunay(points)
>>> np.unique(tri.simplices.ravel())
array([0, 1, 2, 3], dtype=int32)
观察到点 #4(它是重复的)没有作为三角剖分的顶点出现。这种情况被记录下来
>>> tri.coplanar
array([[4, 0, 3]], dtype=int32)
这意味着点 4 位于三角形 0 和顶点 3 附近,但未包含在三角剖分中。
请注意,这种退化不仅可能由于重复点而发生,而且还可能由于更复杂的几何原因而发生,即使在乍一看似乎行为良好的点集中也是如此。
但是,Qhull 具有“QJ”选项,该选项指示它随机扰动输入数据,直到解决退化问题。
>>> tri = Delaunay(points, qhull_options="QJ Pp")
>>> points[tri.simplices]
array([[[1, 0],
[1, 1],
[0, 0]],
[[1, 1],
[1, 1],
[1, 0]],
[[1, 1],
[0, 1],
[0, 0]],
[[0, 1],
[1, 1],
[1, 1]]])
出现了两个新的三角形。但是,我们看到它们是退化的,并且面积为零。
凸包#
凸包是包含给定点集中所有点的最小凸对象。
这些可以通过 scipy.spatial 中的 Qhull 包装器计算,如下所示
>>> from scipy.spatial import ConvexHull
>>> rng = np.random.default_rng()
>>> points = rng.random((30, 2)) # 30 random points in 2-D
>>> hull = ConvexHull(points)
凸包表示为 N 个 1-D 单纯形集,在 2-D 中表示线段。存储方案与上面讨论的 Delaunay 三角剖分中的单纯形完全相同。
我们可以说明上述结果
>>> import matplotlib.pyplot as plt
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> for simplex in hull.simplices:
... plt.plot(points[simplex,0], points[simplex,1], 'k-')
>>> plt.show()
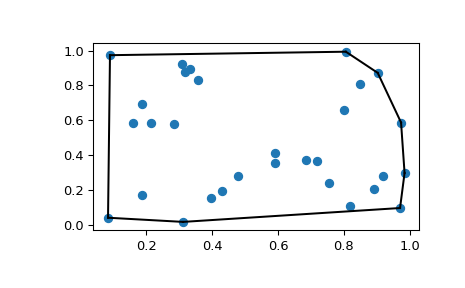
可以使用 scipy.spatial.convex_hull_plot_2d 实现相同的效果。
Voronoi 图#
Voronoi 图是将空间细分为给定点集的最近邻域的细分。
使用 scipy.spatial 有两种方法可以处理此对象。首先,可以使用 KDTree 来回答“哪个点最接近这个点”的问题,并以此方式定义区域
>>> from scipy.spatial import KDTree
>>> points = np.array([[0, 0], [0, 1], [0, 2], [1, 0], [1, 1], [1, 2],
... [2, 0], [2, 1], [2, 2]])
>>> tree = KDTree(points)
>>> tree.query([0.1, 0.1])
(0.14142135623730953, 0)
因此,点 (0.1, 0.1) 属于区域 0。用颜色表示
>>> x = np.linspace(-0.5, 2.5, 31)
>>> y = np.linspace(-0.5, 2.5, 33)
>>> xx, yy = np.meshgrid(x, y)
>>> xy = np.c_[xx.ravel(), yy.ravel()]
>>> import matplotlib.pyplot as plt
>>> dx_half, dy_half = np.diff(x[:2])[0] / 2., np.diff(y[:2])[0] / 2.
>>> x_edges = np.concatenate((x - dx_half, [x[-1] + dx_half]))
>>> y_edges = np.concatenate((y - dy_half, [y[-1] + dy_half]))
>>> plt.pcolormesh(x_edges, y_edges, tree.query(xy)[1].reshape(33, 31), shading='flat')
>>> plt.plot(points[:,0], points[:,1], 'ko')
>>> plt.show()
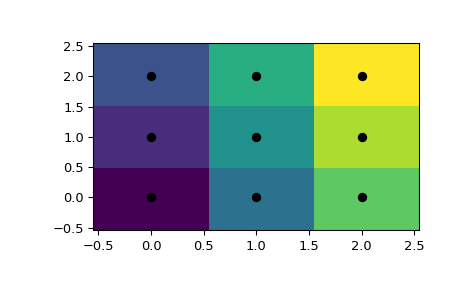
但是,这不会将 Voronoi 图作为几何对象给出。
线和点表示可以通过 scipy.spatial 中的 Qhull 包装器再次获得
>>> from scipy.spatial import Voronoi
>>> vor = Voronoi(points)
>>> vor.vertices
array([[0.5, 0.5],
[0.5, 1.5],
[1.5, 0.5],
[1.5, 1.5]])
Voronoi 顶点表示形成 Voronoi 区域多边形边的点集。在这种情况下,有 9 个不同的区域
>>> vor.regions
[[], [-1, 0], [-1, 1], [1, -1, 0], [3, -1, 2], [-1, 3], [-1, 2], [0, 1, 3, 2], [2, -1, 0], [3, -1, 1]]
负值 -1 再次表示无穷远处的点。实际上,只有一个区域 [0, 1, 3, 2] 是有界的。请注意,由于与上面 Delaunay 三角剖分类似的数值精度问题,Voronoi 区域可能少于输入点。
分离区域的脊(在 2-D 中为线)被描述为与凸包部分类似的单纯形集合
>>> vor.ridge_vertices
[[-1, 0], [-1, 0], [-1, 1], [-1, 1], [0, 1], [-1, 3], [-1, 2], [2, 3], [-1, 3], [-1, 2], [1, 3], [0, 2]]
这些数字表示构成线段的 Voronoi 顶点的索引。 -1 再次是无穷远处的点——只有 12 条线中的 4 条是有界线段,而其他线则延伸到无穷远。
Voronoi 脊线垂直于连接输入点的直线。每个脊线对应哪两个点也被记录下来。
>>> vor.ridge_points
array([[0, 3],
[0, 1],
[2, 5],
[2, 1],
[1, 4],
[7, 8],
[7, 6],
[7, 4],
[8, 5],
[6, 3],
[4, 5],
[4, 3]], dtype=int32)
将这些信息整合在一起,就足以构建完整的图。
我们可以按如下方式绘制它。首先,绘制点和 Voronoi 顶点。
>>> plt.plot(points[:, 0], points[:, 1], 'o')
>>> plt.plot(vor.vertices[:, 0], vor.vertices[:, 1], '*')
>>> plt.xlim(-1, 3); plt.ylim(-1, 3)
绘制有限线段与绘制凸包相同,但现在我们必须注意无限边。
>>> for simplex in vor.ridge_vertices:
... simplex = np.asarray(simplex)
... if np.all(simplex >= 0):
... plt.plot(vor.vertices[simplex, 0], vor.vertices[simplex, 1], 'k-')
延伸到无穷远的脊线需要更多注意。
>>> center = points.mean(axis=0)
>>> for pointidx, simplex in zip(vor.ridge_points, vor.ridge_vertices):
... simplex = np.asarray(simplex)
... if np.any(simplex < 0):
... i = simplex[simplex >= 0][0] # finite end Voronoi vertex
... t = points[pointidx[1]] - points[pointidx[0]] # tangent
... t = t / np.linalg.norm(t)
... n = np.array([-t[1], t[0]]) # normal
... midpoint = points[pointidx].mean(axis=0)
... far_point = vor.vertices[i] + np.sign(np.dot(midpoint - center, n)) * n * 100
... plt.plot([vor.vertices[i,0], far_point[0]],
... [vor.vertices[i,1], far_point[1]], 'k--')
>>> plt.show()
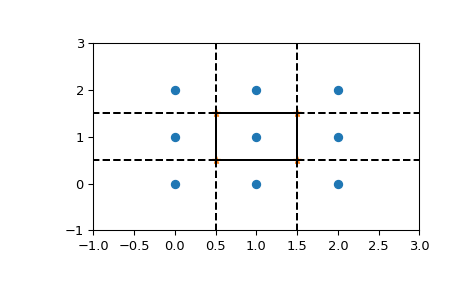
此图也可以使用 scipy.spatial.voronoi_plot_2d 创建。
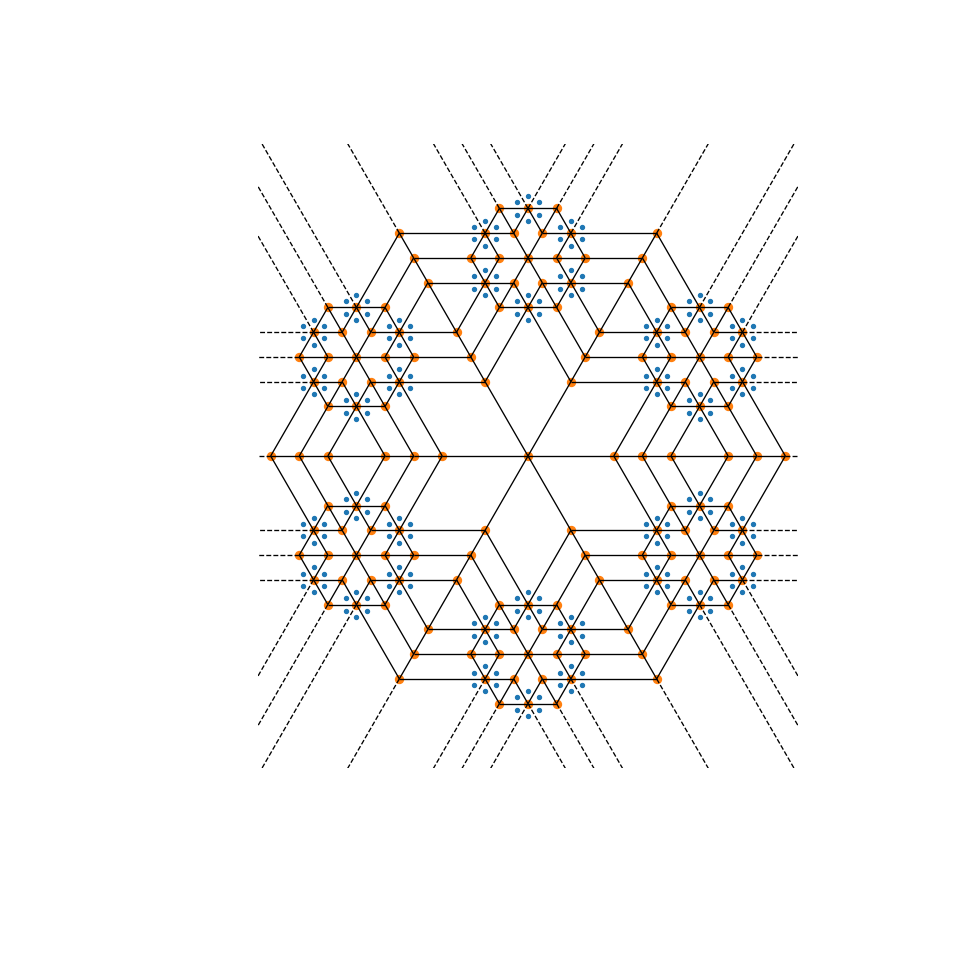
Voronoi 图可以用来创建有趣的生成艺术。尝试使用此 mandala 函数的设置来创建你自己的作品!
>>> import numpy as np
>>> from scipy import spatial
>>> import matplotlib.pyplot as plt
>>> def mandala(n_iter, n_points, radius):
... """Creates a mandala figure using Voronoi tessellations.
...
... Parameters
... ----------
... n_iter : int
... Number of iterations, i.e. how many times the equidistant points will
... be generated.
... n_points : int
... Number of points to draw per iteration.
... radius : scalar
... The radial expansion factor.
...
... Returns
... -------
... fig : matplotlib.Figure instance
...
... Notes
... -----
... This code is adapted from the work of Audrey Roy Greenfeld [1]_ and Carlos
... Focil-Espinosa [2]_, who created beautiful mandalas with Python code. That
... code in turn was based on Antonio Sánchez Chinchón's R code [3]_.
...
... References
... ----------
... .. [1] https://www.codemakesmehappy.com/2019/09/voronoi-mandalas.html
...
... .. [2] https://github.com/CarlosFocil/mandalapy
...
... .. [3] https://github.com/aschinchon/mandalas
...
... """
... fig = plt.figure(figsize=(10, 10))
... ax = fig.add_subplot(111)
... ax.set_axis_off()
... ax.set_aspect('equal', adjustable='box')
...
... angles = np.linspace(0, 2*np.pi * (1 - 1/n_points), num=n_points) + np.pi/2
... # Starting from a single center point, add points iteratively
... xy = np.array([[0, 0]])
... for k in range(n_iter):
... t1 = np.array([])
... t2 = np.array([])
... # Add `n_points` new points around each existing point in this iteration
... for i in range(xy.shape[0]):
... t1 = np.append(t1, xy[i, 0] + radius**k * np.cos(angles))
... t2 = np.append(t2, xy[i, 1] + radius**k * np.sin(angles))
...
... xy = np.column_stack((t1, t2))
...
... # Create the Mandala figure via a Voronoi plot
... spatial.voronoi_plot_2d(spatial.Voronoi(xy), ax=ax)
...
... return fig
>>> # Modify the following parameters in order to get different figures
>>> n_iter = 3
>>> n_points = 6
>>> radius = 4
>>> fig = mandala(n_iter, n_points, radius)
>>> plt.show()