线性代数 (scipy.linalg)

当 SciPy 使用优化的 ATLAS LAPACK 和 BLAS 库构建时，它具有非常快的线性代数功能。如果您深入研究，所有原始 LAPACK 和 BLAS 库都可供您使用，以获得更快的速度。在本节中，将介绍一些更易于使用的这些例程接口。

所有这些线性代数例程都期望一个可以转换为二维数组的对象。这些例程的输出也是二维数组。

scipy.linalg 与 numpy.linalg

scipy.linalg 包含 numpy.linalg 中的所有函数，以及一些 numpy.linalg 中没有的更高级函数。

使用 scipy.linalg 相比 numpy.linalg 的另一个优势是，它始终与 BLAS/LAPACK 支持一起编译，而对于 NumPy 则是可选的。因此，SciPy 版本可能更快，具体取决于 NumPy 的安装方式。

因此，除非您不想将 scipy 作为依赖项添加到您的 numpy 程序中，否则请使用 scipy.linalg 而不是 numpy.linalg。

numpy.matrix 与 2-D numpy.ndarray

表示矩阵的类以及基本运算（如矩阵乘法和转置）是 numpy 的一部分。为了方便起见，我们总结了 numpy.matrix 和 numpy.ndarray 之间的区别。

numpy.matrix 是一个矩阵类，它比 numpy.ndarray 具有更方便的矩阵运算接口。例如，此类支持通过分号的 MATLAB 式创建语法，将矩阵乘法作为 * 运算符的默认值，并且包含 I 和 T 成员，它们用作逆矩阵和转置的快捷方式。

>>> import numpy as np
>>> A = np.asmatrix('[1 2;3 4]')
>>> A
matrix([[1, 2],
        [3, 4]])
>>> A.I
matrix([[-2. ,  1. ],
        [ 1.5, -0.5]])
>>> b = np.asmatrix('[5 6]')
>>> b
matrix([[5, 6]])
>>> b.T
matrix([[5],
        [6]])
>>> A*b.T
matrix([[17],
        [39]])

尽管很方便，但建议不要使用 numpy.matrix 类，因为它没有添加任何无法通过 2-D numpy.ndarray 对象完成的功能，并且可能会导致混淆使用哪个类。例如，上面的代码可以改写为

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.inv(A)
array([[-2. ,  1. ],
      [ 1.5, -0.5]])
>>> b = np.array([[5,6]]) #2D array
>>> b
array([[5, 6]])
>>> b.T
array([[5],
      [6]])
>>> A*b #not matrix multiplication!
array([[ 5, 12],
      [15, 24]])
>>> A.dot(b.T) #matrix multiplication
array([[17],
      [39]])
>>> b = np.array([5,6]) #1D array
>>> b
array([5, 6])
>>> b.T  #not matrix transpose!
array([5, 6])
>>> A.dot(b)  #does not matter for multiplication
array([17, 39])

scipy.linalg 操作可以同样应用于 numpy.matrix 或 2D numpy.ndarray 对象。

基本例程

求逆矩阵

矩阵 \(\mathbf{A}\) 的逆矩阵是矩阵 \(\mathbf{B}\)，使得 \(\mathbf{AB}=\mathbf{I}\)，其中 \(\mathbf{I}\) 是主对角线上为 1 的单位矩阵。通常，\(\mathbf{B}\) 表示为 \(\mathbf{B}=\mathbf{A}^{-1}\)。在 SciPy 中，NumPy 数组 A 的矩阵逆可以使用 linalg.inv (A) 获取，或者如果 A 是一个矩阵，则可以使用 A.I 获取。例如，设

\[\begin{split}\mathbf{A} = \left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right],\end{split}\]

那么

\[\begin{split}\mathbf{A^{-1}} = \frac{1}{25} \left[\begin{array}{ccc} -37 & 9 & 22 \\ 14 & 2 & -9 \\ 4 & -3 & 1 \end{array}\right] = % \left[\begin{array}{ccc} -1.48 & 0.36 & 0.88 \\ 0.56 & 0.08 & -0.36 \\ 0.16 & -0.12 & 0.04 \end{array}\right].\end{split}\]

以下示例演示了在 SciPy 中的计算

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,3,5],[2,5,1],[2,3,8]])
>>> A
array([[1, 3, 5],
      [2, 5, 1],
      [2, 3, 8]])
>>> linalg.inv(A)
array([[-1.48,  0.36,  0.88],
      [ 0.56,  0.08, -0.36],
      [ 0.16, -0.12,  0.04]])
>>> A.dot(linalg.inv(A)) #double check
array([[  1.00000000e+00,  -1.11022302e-16,  -5.55111512e-17],
      [  3.05311332e-16,   1.00000000e+00,   1.87350135e-16],
      [  2.22044605e-16,  -1.11022302e-16,   1.00000000e+00]])

求解线性方程组

使用 scipy 命令 linalg.solve 可以直接求解线性方程组。此命令需要一个输入矩阵和一个右手边向量。然后计算解向量。提供了一个用于输入对称矩阵的选项，这可以在适用时加快处理速度。例如，假设需要求解以下联立方程

\begin{eqnarray*} x + 3y + 5z & = & 10 \\ 2x + 5y + z & = & 8 \\ 2x + 3y + 8z & = & 3 \end{eqnarray*}

可以使用矩阵逆找到解向量

\[\begin{split}\left[\begin{array}{c} x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]^{-1}\left[\begin{array}{c} 10\\ 8\\ 3\end{array}\right]=\frac{1}{25}\left[\begin{array}{c} -232\\ 129\\ 19\end{array}\right]=\left[\begin{array}{c} -9.28\\ 5.16\\ 0.76\end{array}\right].\end{split}\]

但是，最好使用 linalg.solve 命令，它可能更快且数值更稳定。在这种情况下，它会给出与以下示例中显示的相同答案

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> b = np.array([[5], [6]])
>>> b
array([[5],
      [6]])
>>> linalg.inv(A).dot(b)  # slow
array([[-4. ],
      [ 4.5]])
>>> A.dot(linalg.inv(A).dot(b)) - b  # check
array([[  8.88178420e-16],
      [  2.66453526e-15]])
>>> np.linalg.solve(A, b)  # fast
array([[-4. ],
      [ 4.5]])
>>> A.dot(np.linalg.solve(A, b)) - b  # check
array([[ 0.],
      [ 0.]])

求行列式

方阵 \(\mathbf{A}\) 的行列式通常记为 \(\left|\mathbf{A}\right|\)，它是一个在线性代数中经常使用的量。假设 \(a_{ij}\) 是矩阵 \(\mathbf{A}\) 的元素，并令 \(M_{ij}=\left|\mathbf{A}_{ij}\right|\) 为从 \(\mathbf{A}\) 中删除第 \(i^{\textrm{th}}\) 行和第 \(j^{\textrm{th}}\) 列后剩余矩阵的行列式。那么，对于任何行 \(i,\)

\[\left|\mathbf{A}\right|=\sum_{j}\left(-1\right)^{i+j}a_{ij}M_{ij}.\]

这是一种递归定义行列式的方法，其中基本情况定义为接受 \(1\times1\) 矩阵的行列式是唯一的矩阵元素。在 SciPy 中，可以使用 linalg.det 计算行列式。例如，

\[\begin{split}\mathbf{A=}\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]\end{split}\]

的行列式为

\begin{eqnarray*} \left|\mathbf{A}\right| & = & 1\left|\begin{array}{cc} 5 & 1\\ 3 & 8\end{array}\right|-3\left|\begin{array}{cc} 2 & 1\\ 2 & 8\end{array}\right|+5\left|\begin{array}{cc} 2 & 5\\ 2 & 3\end{array}\right|\\ & = & 1\left(5\cdot8-3\cdot1\right)-3\left(2\cdot8-2\cdot1\right)+5\left(2\cdot3-2\cdot5\right)=-25.\end{eqnarray*}.

在 SciPy 中，可以使用以下示例计算：

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.det(A)
-2.0

计算范数

矩阵和向量范数也可以使用 SciPy 计算。可以使用 linalg.norm 函数的不同参数来计算各种范数定义。此函数接受一个秩 1（向量）或秩 2（矩阵）数组和一个可选的 order 参数（默认值为 2）。根据这些输入，将计算请求阶数的向量或矩阵范数。

对于向量 x，order 参数可以是任何实数，包括 inf 或 -inf。计算的范数为

\[\begin{split}\left\Vert \mathbf{x}\right\Vert =\left\{ \begin{array}{cc} \max\left|x_{i}\right| & \textrm{ord}=\textrm{inf}\\ \min\left|x_{i}\right| & \textrm{ord}=-\textrm{inf}\\ \left(\sum_{i}\left|x_{i}\right|^{\textrm{ord}}\right)^{1/\textrm{ord}} & \left|\textrm{ord}\right|<\infty.\end{array}\right.\end{split}\]

对于矩阵 \(\mathbf{A}\)，范数的有效值只有 \(\pm2,\pm1,\) \(\pm\) inf 和 'fro'（或 'f'）。因此，

\[\begin{split}\left\Vert \mathbf{A}\right\Vert =\left\{ \begin{array}{cc} \max_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=\textrm{inf}\\ \min_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=-\textrm{inf}\\ \max_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=1\\ \min_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=-1\\ \max\sigma_{i} & \textrm{ord}=2\\ \min\sigma_{i} & \textrm{ord}=-2\\ \sqrt{\textrm{trace}\left(\mathbf{A}^{H}\mathbf{A}\right)} & \textrm{ord}=\textrm{'fro'}\end{array}\right.\end{split}\]

其中 \(\sigma_{i}\) 是 \(\mathbf{A}\) 的奇异值。

示例

>>> import numpy as np
>>> from scipy import linalg
>>> A=np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.norm(A)
5.4772255750516612
>>> linalg.norm(A,'fro') # frobenius norm is the default
5.4772255750516612
>>> linalg.norm(A,1) # L1 norm (max column sum)
6
>>> linalg.norm(A,-1)
4
>>> linalg.norm(A,np.inf) # L inf norm (max row sum)
7

求解线性最小二乘问题和伪逆

线性最小二乘问题出现在应用数学的许多分支中。在这个问题中，我们寻找一组线性缩放系数，使模型能够拟合数据。具体来说，我们假设数据 \(y_{i}\) 与数据 \(\mathbf{x}_{i}\) 通过一组系数 \(c_{j}\) 和模型函数 \(f_{j}\left(\mathbf{x}_{i}\right)\) 以及模型

\[y_{i}=\sum_{j}c_{j}f_{j}\left(\mathbf{x}_{i}\right)+\epsilon_{i},\]

其中 \(\epsilon_{i}\) 表示数据中的不确定性。最小二乘法的策略是选择系数 \(c_{j}\) 来最小化

\[J\left(\mathbf{c}\right)=\sum_{i}\left|y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right|^{2}.\]

理论上，全局最小值将在以下情况下出现

\[\frac{\partial J}{\partial c_{n}^{*}}=0=\sum_{i}\left(y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right)\left(-f_{n}^{*}\left(x_{i}\right)\right)\]

或

\begin{eqnarray*} \sum_{j}c_{j}\sum_{i}f_{j}\left(x_{i}\right)f_{n}^{*}\left(x_{i}\right) & = & \sum_{i}y_{i}f_{n}^{*}\left(x_{i}\right)\\ \mathbf{A}^{H}\mathbf{Ac} & = & \mathbf{A}^{H}\mathbf{y}\end{eqnarray*},

其中

\[\left\{ \mathbf{A}\right\} _{ij}=f_{j}\left(x_{i}\right).\]

当 \(\mathbf{A^{H}A}\) 可逆时，则

\[\mathbf{c}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H}\mathbf{y}=\mathbf{A}^{\dagger}\mathbf{y},\]

其中 \(\mathbf{A}^{\dagger}\) 称为 \(\mathbf{A}.\) 的伪逆。注意，使用这个定义的 \(\mathbf{A}\)，模型可以写成

\[\mathbf{y}=\mathbf{Ac}+\boldsymbol{\epsilon}.\]

命令 linalg.lstsq 将解决给定 \(\mathbf{A}\) 和 \(\mathbf{y}\) 的线性最小二乘问题，求解 \(\mathbf{c}\)。此外，linalg.pinv 将在给定 \(\mathbf{A}\) 的情况下找到 \(\mathbf{A}^{\dagger}\)。

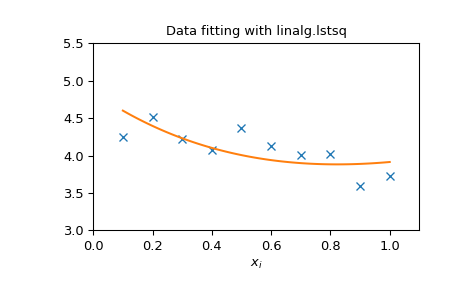
以下示例和图示演示了使用 linalg.lstsq 和 linalg.pinv 解决数据拟合问题。以下显示的数据使用模型生成

\[y_{i}=c_{1}e^{-x_{i}}+c_{2}x_{i},\]

其中 \(x_{i}=0.1i\) 对于 \(i=1\ldots10\)，\(c_{1}=5\)，以及 \(c_{2}=4.\) 噪声被添加到 \(y_{i}\) 中，系数 \(c_{1}\) 和 \(c_{2}\) 使用线性最小二乘法估计。

>>> import numpy as np
>>> from scipy import linalg
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

>>> c1, c2 = 5.0, 2.0
>>> i = np.r_[1:11]
>>> xi = 0.1*i
>>> yi = c1*np.exp(-xi) + c2*xi
>>> zi = yi + 0.05 * np.max(yi) * rng.standard_normal(len(yi))

>>> A = np.c_[np.exp(-xi)[:, np.newaxis], xi[:, np.newaxis]]
>>> c, resid, rank, sigma = linalg.lstsq(A, zi)

>>> xi2 = np.r_[0.1:1.0:100j]
>>> yi2 = c[0]*np.exp(-xi2) + c[1]*xi2

>>> plt.plot(xi,zi,'x',xi2,yi2)
>>> plt.axis([0,1.1,3.0,5.5])
>>> plt.xlabel('$x_i$')
>>> plt.title('Data fitting with linalg.lstsq')
>>> plt.show()

广义逆

广义逆是使用命令 linalg.pinv 计算的。设 \(\mathbf{A}\) 为一个 \(M\times N\) 矩阵，那么如果 \(M>N\)，广义逆为

\[\mathbf{A}^{\dagger}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H},\]

而如果 \(M<N\) 矩阵，广义逆为

\[\mathbf{A}^{\#}=\mathbf{A}^{H}\left(\mathbf{A}\mathbf{A}^{H}\right)^{-1}.\]

在 \(M=N\) 的情况下，则

\[\mathbf{A}^{\dagger}=\mathbf{A}^{\#}=\mathbf{A}^{-1},\]

只要 \(\mathbf{A}\) 可逆。

分解

在许多应用中，使用其他表示形式分解矩阵非常有用。SciPy 支持几种分解。

特征值和特征向量

特征值-特征向量问题是最常用的线性代数运算之一。在一个流行的形式中，特征值-特征向量问题是为某个方阵 \(\mathbf{A}\) 寻找标量 \(\lambda\) 和相应的向量 \(\mathbf{v}\)，使得

\[\mathbf{Av}=\lambda\mathbf{v}.\]

对于一个 \(N\times N\) 矩阵，有 \(N\) 个（不一定是不同的）特征值——（特征）多项式的根

\[\left|\mathbf{A}-\lambda\mathbf{I}\right|=0.\]

特征向量 \(\mathbf{v}\) 有时也被称为右特征向量，以区别于另一组满足以下条件的左特征向量

\[\mathbf{v}_{L}^{H}\mathbf{A}=\lambda\mathbf{v}_{L}^{H}\]

或

\[\mathbf{A}^{H}\mathbf{v}_{L}=\lambda^{*}\mathbf{v}_{L}.\]

使用默认的可选参数，命令 linalg.eig 返回 \(\lambda\) 和 \(\mathbf{v}.\) 但是，它也可以返回 \(\mathbf{v}_{L}\) 和仅 \(\lambda\) 本身（linalg.eigvals 也只返回 \(\lambda\)）。

此外，linalg.eig 还可以解决更一般的特征值问题

\begin{eqnarray*} \mathbf{Av} & = & \lambda\mathbf{Bv}\\ \mathbf{A}^{H}\mathbf{v}_{L} & = & \lambda^{*}\mathbf{B}^{H}\mathbf{v}_{L}\end{eqnarray*}

对于方阵 \(\mathbf{A}\) 和 \(\mathbf{B}.\) 标准特征值问题是 \(\mathbf{B}=\mathbf{I}.\) 的一般特征值问题的特例。当广义特征值问题可以求解时，它提供了 \(\mathbf{A}\) 的分解，如下所示：

\[\mathbf{A}=\mathbf{BV}\boldsymbol{\Lambda}\mathbf{V}^{-1},\]

其中 \(\mathbf{V}\) 是将特征向量收集到列中的矩阵，而 \(\boldsymbol{\Lambda}\) 是特征值的对角矩阵。

根据定义，特征向量仅在常数比例因子下定义。在 SciPy 中，特征向量的比例因子选择为 \(\left\Vert \mathbf{v}\right\Vert ^{2}=\sum_{i}v_{i}^{2}=1.\)

例如，考虑求解矩阵的特征值和特征向量

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccc} 1 & 5 & 2\\ 2 & 4 & 1\\ 3 & 6 & 2\end{array}\right].\end{split}\]

特征多项式为

\begin{eqnarray*} \left|\mathbf{A}-\lambda\mathbf{I}\right| & = & \left(1-\lambda\right)\left[\left(4-\lambda\right)\left(2-\lambda\right)-6\right]-\\ & & 5\left[2\left(2-\lambda\right)-3\right]+2\left[12-3\left(4-\lambda\right)\right]\\ & = & -\lambda^{3}+7\lambda^{2}+8\lambda-3.\end{eqnarray*}

该多项式的根是 \(\mathbf{A}\) 的特征值

\begin{eqnarray*} \lambda_{1} & = & 7.9579\\ \lambda_{2} & = & -1.2577\\ \lambda_{3} & = & 0.2997.\end{eqnarray*}

可以使用原始方程找到与每个特征值对应的特征向量。然后可以找到与这些特征值相关的特征向量。

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> la, v = linalg.eig(A)
>>> l1, l2 = la
>>> print(l1, l2)   # eigenvalues
(-0.3722813232690143+0j) (5.372281323269014+0j)
>>> print(v[:, 0])   # first eigenvector
[-0.82456484  0.56576746]
>>> print(v[:, 1])   # second eigenvector
[-0.41597356 -0.90937671]
>>> print(np.sum(abs(v**2), axis=0))  # eigenvectors are unitary
[1. 1.]
>>> v1 = np.array(v[:, 0]).T
>>> print(linalg.norm(A.dot(v1) - l1*v1))  # check the computation
3.23682852457e-16

奇异值分解

奇异值分解 (SVD) 可以被认为是对非方阵的特征值问题的扩展。令 \(\mathbf{A}\) 为一个 \(M\times N\) 矩阵，其中 \(M\) 和 \(N\) 为任意值。矩阵 \(\mathbf{A}^{H}\mathbf{A}\) 和 \(\mathbf{A}\mathbf{A}^{H}\) 是大小分别为 \(N\times N\) 和 \(M\times M\) 的方阵厄米矩阵 [1]。已知方阵厄米矩阵的特征值为实数且非负。此外，\(\mathbf{A}^{H}\mathbf{A}\) 和 \(\mathbf{A}\mathbf{A}^{H}.\) 的非零特征值最多有 \(\min\left(M,N\right)\) 个相同的值。将这些正特征值定义为 \(\sigma_{i}^{2}.\) 它们的平方根被称为 \(\mathbf{A}.\) 的奇异值。将 \(\mathbf{A}^{H}\mathbf{A}\) 的特征向量按列收集到一个 \(N\times N\) 的酉矩阵 [2] \(\mathbf{V}\) 中，而将 \(\mathbf{A}\mathbf{A}^{H}\) 的特征向量按列收集到酉矩阵 \(\mathbf{U}\) 中，将奇异值收集到一个 \(M\times N\) 的零矩阵 \(\mathbf{\boldsymbol{\Sigma}}\) 中，其主对角线元素设置为奇异值。然后

\[\mathbf{A=U}\boldsymbol{\Sigma}\mathbf{V}^{H}\]

是 \(\mathbf{A}.\) 的奇异值分解。每个矩阵都有一个奇异值分解。有时，奇异值被称为 \(\mathbf{A}.\) 的谱。命令 linalg.svd 将返回 \(\mathbf{U}\)、\(\mathbf{V}^{H}\) 和 \(\sigma_{i}\) 作为奇异值的数组。要获得矩阵 \(\boldsymbol{\Sigma}\)，请使用 linalg.diagsvd。以下示例说明了 linalg.svd 的用法

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2,3],[4,5,6]])
>>> A
array([[1, 2, 3],
      [4, 5, 6]])
>>> M,N = A.shape
>>> U,s,Vh = linalg.svd(A)
>>> Sig = linalg.diagsvd(s,M,N)
>>> U, Vh = U, Vh
>>> U
array([[-0.3863177 , -0.92236578],
      [-0.92236578,  0.3863177 ]])
>>> Sig
array([[ 9.508032  ,  0.        ,  0.        ],
      [ 0.        ,  0.77286964,  0.        ]])
>>> Vh
array([[-0.42866713, -0.56630692, -0.7039467 ],
      [ 0.80596391,  0.11238241, -0.58119908],
      [ 0.40824829, -0.81649658,  0.40824829]])
>>> U.dot(Sig.dot(Vh)) #check computation
array([[ 1.,  2.,  3.],
      [ 4.,  5.,  6.]])

[1]

厄米矩阵 \(\mathbf{D}\) 满足 \(\mathbf{D}^{H}=\mathbf{D}.\)

[2]

酉矩阵 \(\mathbf{D}\) 满足 \(\mathbf{D}^{H}\mathbf{D}=\mathbf{I}=\mathbf{D}\mathbf{D}^{H}\)，因此 \(\mathbf{D}^{-1}=\mathbf{D}^{H}.\)

LU 分解

LU 分解找到 \(M\times N\) 矩阵 \(\mathbf{A}\) 的表示形式为

\[\mathbf{A}=\mathbf{P}\,\mathbf{L}\,\mathbf{U},\]

其中 \(\mathbf{P}\) 是一个 \(M\times M\) 置换矩阵（单位矩阵的行置换），\(\mathbf{L}\) 是一个 \(M\times K\) 下三角或梯形矩阵（\(K=\min\left(M,N\right)\)）且对角线元素为 1，\(\mathbf{U}\) 是一个上三角或梯形矩阵。SciPy 中用于此分解的命令是 linalg.lu.

这种分解通常用于求解许多联立方程，其中左侧不变，但右侧变化。例如，假设我们要求解

\[\mathbf{A}\mathbf{x}_{i}=\mathbf{b}_{i}\]

对于许多不同的 \(\mathbf{b}_{i}\)。LU 分解允许将其写成

\[\mathbf{PLUx}_{i}=\mathbf{b}_{i}.\]

由于 \(\mathbf{L}\) 是下三角矩阵，因此可以使用前向和后向替换非常快速地求解 \(\mathbf{U}\mathbf{x}_{i}\)，最终求解 \(\mathbf{x}_{i}\)。对 \(\mathbf{A}\) 进行因式分解的初始时间允许在未来快速求解类似的方程组。如果执行 LU 分解的目的是为了求解线性方程组，那么应该使用命令 linalg.lu_factor，然后重复使用命令 linalg.lu_solve 来为每个新的右侧求解方程组。

Cholesky 分解

Cholesky 分解是 LU 分解的一种特殊情况，适用于 Hermitian 正定矩阵。当 \(\mathbf{A}=\mathbf{A}^{H}\) 且 \(\mathbf{x}^{H}\mathbf{Ax}\geq0\) 对于所有 \(\mathbf{x}\) 成立时，可以找到 \(\mathbf{A}\) 的分解，使得

\begin{eqnarray*} \mathbf{A} & = & \mathbf{U}^{H}\mathbf{U}\\ \mathbf{A} & = & \mathbf{L}\mathbf{L}^{H}\end{eqnarray*},

其中 \(\mathbf{L}\) 是下三角矩阵，\(\mathbf{U}\) 是上三角矩阵。请注意 \(\mathbf{L}=\mathbf{U}^{H}.\) 命令 linalg.cholesky 计算 Cholesky 分解。为了使用 Cholesky 分解来求解方程组，还有 linalg.cho_factor 和 linalg.cho_solve 函数，它们的工作方式类似于它们的 LU 分解对应函数。

QR 分解

QR 分解（有时称为极分解）适用于任何 \(M\times N\) 矩阵，并找到一个 \(M\times M\) 酉矩阵 \(\mathbf{Q}\) 和一个 \(M\times N\) 上梯形矩阵 \(\mathbf{R}\)，使得

\[\mathbf{A=QR}.\]

请注意，如果已知 \(\mathbf{A}\) 的 SVD，则可以找到 QR 分解。

\[\mathbf{A}=\mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^{H}=\mathbf{QR}\]

意味着 \(\mathbf{Q}=\mathbf{U}\) 和 \(\mathbf{R}=\boldsymbol{\Sigma}\mathbf{V}^{H}.\) 但是请注意，在 SciPy 中，使用独立的算法来查找 QR 和 SVD 分解。QR 分解的命令是 linalg.qr.

舒尔分解

对于一个方阵 \(N\times N\) 矩阵 \(\mathbf{A}\)，舒尔分解找到（不一定是唯一的）矩阵 \(\mathbf{T}\) 和 \(\mathbf{Z}\)，使得

\[\mathbf{A}=\mathbf{ZT}\mathbf{Z}^{H},\]

其中 \(\mathbf{Z}\) 是一个酉矩阵，\(\mathbf{T}\) 是上三角矩阵或准上三角矩阵，具体取决于是否请求实 Schur 形式或复 Schur 形式。对于实 Schur 形式，当 \(\mathbf{A}\) 为实数时，\(\mathbf{T}\) 和 \(\mathbf{Z}\) 都是实数。当 \(\mathbf{A}\) 是实数矩阵时，实 Schur 形式仅为准上三角形式，因为对应于任何复数特征值的 \(2\times2\) 块从主对角线突出。命令 linalg.schur 找到 Schur 分解，而命令 linalg.rsf2csf 将 \(\mathbf{T}\) 和 \(\mathbf{Z}\) 从实 Schur 形式转换为复 Schur 形式。Schur 形式在计算矩阵函数时特别有用。

以下示例说明了 Schur 分解

>>> from scipy import linalg
>>> A = np.asmatrix('[1 3 2; 1 4 5; 2 3 6]')
>>> T, Z = linalg.schur(A)
>>> T1, Z1 = linalg.schur(A, 'complex')
>>> T2, Z2 = linalg.rsf2csf(T, Z)
>>> T
array([[ 9.90012467,  1.78947961, -0.65498528],
       [ 0.        ,  0.54993766, -1.57754789],
       [ 0.        ,  0.51260928,  0.54993766]])
>>> T2
array([[ 9.90012467+0.00000000e+00j, -0.32436598+1.55463542e+00j,
        -0.88619748+5.69027615e-01j],
       [ 0.        +0.00000000e+00j,  0.54993766+8.99258408e-01j,
         1.06493862+3.05311332e-16j],
       [ 0.        +0.00000000e+00j,  0.        +0.00000000e+00j,
         0.54993766-8.99258408e-01j]])
>>> abs(T1 - T2) # different
array([[  1.06604538e-14,   2.06969555e+00,   1.69375747e+00],  # may vary
       [  0.00000000e+00,   1.33688556e-15,   4.74146496e-01],
       [  0.00000000e+00,   0.00000000e+00,   1.13220977e-15]])
>>> abs(Z1 - Z2) # different
array([[ 0.06833781,  0.88091091,  0.79568503],    # may vary
       [ 0.11857169,  0.44491892,  0.99594171],
       [ 0.12624999,  0.60264117,  0.77257633]])
>>> T, Z, T1, Z1, T2, Z2 = map(np.asmatrix,(T,Z,T1,Z1,T2,Z2))
>>> abs(A - Z*T*Z.H)  # same
matrix([[  5.55111512e-16,   1.77635684e-15,   2.22044605e-15],
        [  0.00000000e+00,   3.99680289e-15,   8.88178420e-16],
        [  1.11022302e-15,   4.44089210e-16,   3.55271368e-15]])
>>> abs(A - Z1*T1*Z1.H)  # same
matrix([[  4.26993904e-15,   6.21793362e-15,   8.00007092e-15],
        [  5.77945386e-15,   6.21798014e-15,   1.06653681e-14],
        [  7.16681444e-15,   8.90271058e-15,   1.77635764e-14]])
>>> abs(A - Z2*T2*Z2.H)  # same
matrix([[  6.02594127e-16,   1.77648931e-15,   2.22506907e-15],
        [  2.46275555e-16,   3.99684548e-15,   8.91642616e-16],
        [  8.88225111e-16,   8.88312432e-16,   4.44104848e-15]])

插值分解

scipy.linalg.interpolative 包含用于计算矩阵的插值分解 (ID) 的例程。对于秩为 \(k \leq \min \{ m, n \}\) 的矩阵 \(A \in \mathbb{C}^{m \times n}\)，这是一个分解

\[A \Pi = \begin{bmatrix} A \Pi_{1} & A \Pi_{2} \end{bmatrix} = A \Pi_{1} \begin{bmatrix} I & T \end{bmatrix},\]

其中 \(\Pi = [\Pi_{1}, \Pi_{2}]\) 是一个置换矩阵，其中 \(\Pi_{1} \in \{ 0, 1 \}^{n \times k}\)，即 \(A \Pi_{2} = A \Pi_{1} T\)。这等效于写成 \(A = BP\)，其中 \(B = A \Pi_{1}\) 和 \(P = [I, T] \Pi^{\mathsf{T}}\) 分别是骨架和插值矩阵。

另请参阅

scipy.linalg.interpolative — 了解更多信息。

矩阵函数

考虑函数 \(f\left(x\right)\) 的泰勒级数展开

\[f\left(x\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}x^{k}.\]

可以使用这个泰勒级数为方阵 \(\mathbf{A}\) 定义矩阵函数

\[f\left(\mathbf{A}\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}\mathbf{A}^{k}.\]

注意

虽然这为矩阵函数提供了一个有用的表示，但它很少是计算矩阵函数的最佳方法。特别是，如果矩阵不可对角化，结果可能不准确。

指数和对数函数

矩阵指数是最常见的矩阵函数之一。实现矩阵指数的首选方法是使用缩放和 \(e^{x}\) 的 Padé 近似。此算法在 linalg.expm 中实现。

矩阵指数的逆是矩阵对数，定义为矩阵指数的逆

\[\mathbf{A}\equiv\exp\left(\log\left(\mathbf{A}\right)\right).\]

可以使用 linalg.logm 获取矩阵对数。

三角函数

三角函数 \(\sin\)、\(\cos\) 和 \(\tan\) 在 linalg.sinm、linalg.cosm 和 linalg.tanm 中分别针对矩阵实现。可以使用欧拉恒等式定义矩阵正弦和余弦

\begin{eqnarray*} \sin\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}-e^{-j\mathbf{A}}}{2j}\\ \cos\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}+e^{-j\mathbf{A}}}{2}.\end{eqnarray*}

正切为

\[\tan\left(x\right)=\frac{\sin\left(x\right)}{\cos\left(x\right)}=\left[\cos\left(x\right)\right]^{-1}\sin\left(x\right)\]

因此，矩阵正切定义为

\[\left[\cos\left(\mathbf{A}\right)\right]^{-1}\sin\left(\mathbf{A}\right).\]

双曲三角函数

双曲三角函数，\(\sinh\)，\(\cosh\)，和\(\tanh\)，也可以使用熟悉的定义为矩阵定义

\begin{eqnarray*} \sinh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}-e^{-\mathbf{A}}}{2}\\ \cosh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}+e^{-\mathbf{A}}}{2}\\ \tanh\left(\mathbf{A}\right) & = & \left[\cosh\left(\mathbf{A}\right)\right]^{-1}\sinh\left(\mathbf{A}\right).\end{eqnarray*}

这些矩阵函数可以使用 linalg.sinhm，linalg.coshm，和 linalg.tanhm 找到。

任意函数

最后，任何接受一个复数并返回一个复数的任意函数都可以使用命令 linalg.funm 作为矩阵函数调用。此命令接受矩阵和任意 Python 函数。然后，它实现 Golub 和 Van Loan 的书“矩阵计算”中的一种算法，使用 Schur 分解计算应用于矩阵的函数。请注意，该函数需要接受复数作为输入才能与该算法一起使用。例如，以下代码计算应用于矩阵的零阶贝塞尔函数。

>>> from scipy import special, linalg
>>> rng = np.random.default_rng()
>>> A = rng.random((3, 3))
>>> B = linalg.funm(A, lambda x: special.jv(0, x))
>>> A
array([[0.06369197, 0.90647174, 0.98024544],
       [0.68752227, 0.5604377 , 0.49142032],
       [0.86754578, 0.9746787 , 0.37932682]])
>>> B
array([[ 0.6929219 , -0.29728805, -0.15930896],
       [-0.16226043,  0.71967826, -0.22709386],
       [-0.19945564, -0.33379957,  0.70259022]])
>>> linalg.eigvals(A)
array([ 1.94835336+0.j, -0.72219681+0.j, -0.22270006+0.j])
>>> special.jv(0, linalg.eigvals(A))
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])
>>> linalg.eigvals(B)
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])

请注意，由于矩阵解析函数的定义方式，贝塞尔函数作用于矩阵特征值。

特殊矩阵

SciPy 和 NumPy 提供了几个用于创建工程和科学中经常使用的特殊矩阵的函数。

类型	函数	描述
块对角线	scipy.linalg.block_diag	从提供的数组创建块对角矩阵。
循环	scipy.linalg.circulant	创建循环矩阵。
伴随	scipy.linalg.companion	创建伴随矩阵。
卷积	scipy.linalg.convolution_matrix	创建卷积矩阵。
离散傅里叶	scipy.linalg.dft	创建离散傅里叶变换矩阵。
费德勒	scipy.linalg.fiedler	创建对称费德勒矩阵。
费德勒伴随	scipy.linalg.fiedler_companion	创建费德勒伴随矩阵。
阿达玛	scipy.linalg.hadamard	创建阿达玛矩阵。
汉克尔	scipy.linalg.hankel	创建汉克尔矩阵。
赫尔默特	scipy.linalg.helmert	创建赫尔默特矩阵。
希尔伯特	scipy.linalg.hilbert	创建希尔伯特矩阵。
逆希尔伯特	scipy.linalg.invhilbert	创建希尔伯特矩阵的逆矩阵。
莱斯利	scipy.linalg.leslie	创建莱斯利矩阵。
帕斯卡	scipy.linalg.pascal	创建帕斯卡矩阵。
逆帕斯卡	scipy.linalg.invpascal	创建帕斯卡矩阵的逆矩阵。
托普利茨	scipy.linalg.toeplitz	创建托普利茨矩阵。
范德蒙德	numpy.vander	创建范德蒙德矩阵。

有关这些函数使用示例，请参阅其各自的文档字符串。