scipy.signal.windows.
taylor#
- scipy.signal.windows.taylor(M, nbar=4, sll=30, norm=True, sym=True, *, xp=None, device=None)[source]#
返回 Taylor 窗。
对于参数化数量的近端旁瓣,Taylor 窗锥形函数近似于 Dolph-Chebyshev 窗的恒定旁瓣电平,但允许超过 [2] 的锥形。
SAR(合成孔径雷达)社区通常使用 Taylor 加权进行图像形成处理,因为它提供了强大的、可选的旁瓣抑制,并且使主瓣的加宽最小 [1]。
- 参数:
- Mint
输出窗口中的点数。如果为零,则返回一个空数组。当为负数时,会抛出异常。
- nbarint, 可选
与主瓣相邻的近乎恒定电平旁瓣数。
- sllfloat, 可选
相对于主瓣的直流增益,旁瓣电平所需的抑制分贝 (dB)。这应该是一个正数。
- normbool, 可选
当为 True(默认)时,将窗口除以奇数长度窗口的最大(中间)值,或偶数长度窗口的两个重复中间值之间的值,以便所有值都小于或等于 1。当为 False 时,直流增益将保持在 1 (0 dB),旁瓣将降低 sll dB。
- symbool, 可选
当为 True(默认)时,生成一个对称窗口,用于滤波器设计。当为 False 时,生成一个周期性窗口,用于频谱分析。
- xparray_namespace, 可选
可选数组命名空间。应与数组 API 标准兼容,或由 array-api-compat 支持。默认:
numpy- 设备:any
输出的可选设备规范。应与
xp中的支持设备规范之一匹配。
- 返回:
- outarray
窗口。当 norm 为 True(默认)时,最大值被标准化为 1(但如果 M 为偶数且 sym 为 True,则不会出现值 1)。
参考
[1]W. Carrara, R. Goodman 和 R. Majewski,“聚束合成孔径雷达:信号处理算法”,第 512-513 页,1995 年 7 月。
示例
绘制窗口及其频率响应
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt
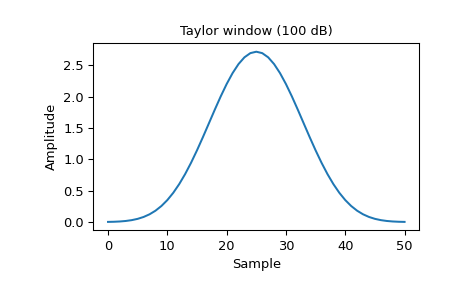
>>> window = signal.windows.taylor(51, nbar=20, sll=100, norm=False) >>> plt.plot(window) >>> plt.title("Taylor window (100 dB)") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
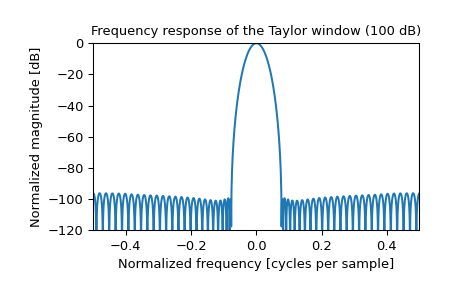
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title("Frequency response of the Taylor window (100 dB)") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")