scipy.signal.windows.

tukey

scipy.signal.windows.tukey(M, alpha=0.5, sym=True)

返回一个 Tukey 窗口，也称为锥形余弦窗口。

参数:

Mint

输出窗口中的点数。 如果为零，则返回一个空数组。 如果为负数，则会抛出异常。

alphafloat, 可选

Tukey 窗口的形状参数，表示窗口内余弦锥形区域的比例。 如果为零，则 Tukey 窗口等效于矩形窗口。 如果为一，则 Tukey 窗口等效于 Hann 窗口。

symbool, 可选

当为 True（默认值）时，生成用于滤波器设计的对称窗口。当为 False 时，生成用于频谱分析的周期窗口。

返回:

wndarray

窗口，最大值归一化为 1（但如果 M 为偶数且 sym 为 True，则不会出现值 1）。

参考

[1]

Harris, Fredric J. (1978 年 1 月)。 “关于使用窗口进行离散傅里叶变换的谐波分析”。 IEEE 会刊 66 (1): 51-83。 DOI:10.1109/PROC.1978.10837

[2]

维基百科，“窗口函数”，https://en.wikipedia.org/wiki/Window_function#Tukey_window

示例

在您的浏览器中尝试一下！

绘制窗口及其频率响应

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

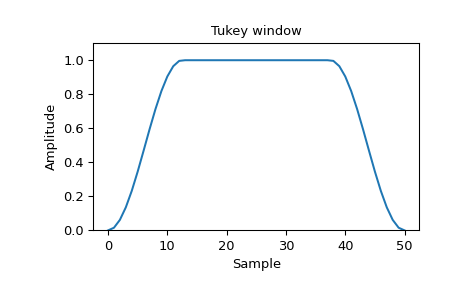
>>> window = signal.windows.tukey(51)
>>> plt.plot(window)
>>> plt.title("Tukey window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")
>>> plt.ylim([0, 1.1])

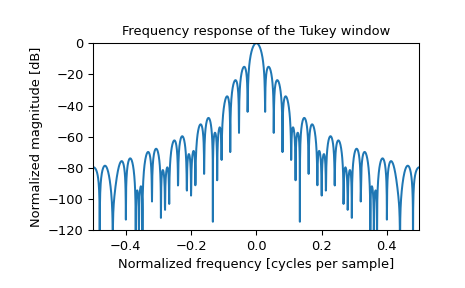
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Tukey window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

返回在新标签页中打开