scipy.signal.windows.

general_hamming

scipy.signal.windows.general_hamming(M, alpha, sym=True, *, xp=None, device=None)

返回广义汉明窗。

广义汉明窗是通过将矩形窗乘以余弦函数的一个周期来构造的 [1]。

参数:

Mint

输出窗口中的点数。如果为零，则返回一个空数组。当它为负数时，会抛出一个异常。

alphafloat

窗口系数，\(\alpha\)

symbool, optional

当为 True (默认) 时，生成一个对称窗口，用于滤波器设计。当为 False 时，生成一个周期性窗口，用于频谱分析。

xparray_namespace, optional

可选的数组命名空间。应与数组 API 标准兼容，或由 array-api-compat 支持。默认值：numpy

device: any

输出的可选设备规范。应与 xp 中支持的设备规范之一匹配。

返回值:

wndarray

窗口，最大值归一化为 1（尽管如果 M 为偶数且 sym 为 True，则不会出现值 1）。

参见

hamming, hann

注释

广义汉明窗定义为

\[w(n) = \alpha - \left(1 - \alpha\right) \cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

常见的汉明窗和汉恩窗都是广义汉明窗的特殊情况，其中 \(\alpha\) = 0.54 和 \(\alpha\) = 0.5，分别 [2]。

参考文献

[1]

DSPRelated, “Generalized Hamming Window Family”, https://www.dsprelated.com/freebooks/sasp/Generalized_Hamming_Window_Family.html

[2]

Wikipedia, “Window function”, https://en.wikipedia.org/wiki/Window_function

[3]

Riccardo Piantanida ESA, “Sentinel-1 Level 1 Detailed Algorithm Definition”, https://sentinel.esa.int/documents/247904/1877131/Sentinel-1-Level-1-Detailed-Algorithm-Definition

[4]

Matthieu Bourbigot ESA, “Sentinel-1 Product Definition”, https://sentinel.esa.int/documents/247904/1877131/Sentinel-1-Product-Definition

示例

在您的浏览器中尝试一下！

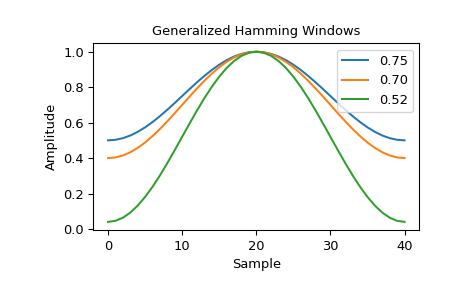
Sentinel-1A/B 仪器处理设施在星载合成孔径雷达 (SAR) 数据的处理中使用广义汉明窗 [3]。 该设施根据 SAR 仪器的运行模式使用不同的 \(\alpha\) 参数值。 一些常见的 \(\alpha\) 值包括 0.75、0.7 和 0.52 [4]。 作为一个例子，我们绘制这些不同的窗口。

>>> import numpy as np
>>> from scipy.signal.windows import general_hamming
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> fig1, spatial_plot = plt.subplots()
>>> spatial_plot.set_title("Generalized Hamming Windows")
>>> spatial_plot.set_ylabel("Amplitude")
>>> spatial_plot.set_xlabel("Sample")

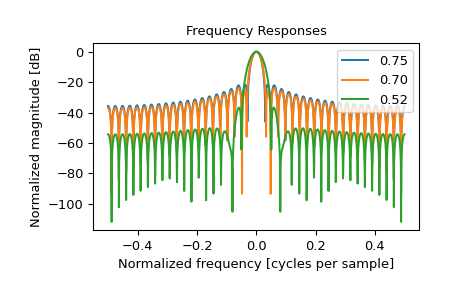
>>> fig2, freq_plot = plt.subplots()
>>> freq_plot.set_title("Frequency Responses")
>>> freq_plot.set_ylabel("Normalized magnitude [dB]")
>>> freq_plot.set_xlabel("Normalized frequency [cycles per sample]")

>>> for alpha in [0.75, 0.7, 0.52]:
...     window = general_hamming(41, alpha)
...     spatial_plot.plot(window, label="{:.2f}".format(alpha))
...     A = fft(window, 2048) / (len(window)/2.0)
...     freq = np.linspace(-0.5, 0.5, len(A))
...     response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
...     freq_plot.plot(freq, response, label="{:.2f}".format(alpha))
>>> freq_plot.legend(loc="upper right")
>>> spatial_plot.legend(loc="upper right")

返回在新标签页中打开