scipy.interpolate.

UnivariateSpline#

class scipy.interpolate.UnivariateSpline(x, y, w=None, bbox=[None, None], k=3, s=None, ext=0, check_finite=False)[源代码]#

对给定的数据集进行一维平滑样条拟合。

将度数为 k 的样条 y = spl（x）拟合到所提供的 x、y 数据。s 通过指定平滑条件来指定结点数。

参数:

x(N,) 数组类似物

1-D 独立输入数据数组。必须增加；如果 s 为 0，则必须严格增加。

y(N,) 数组类似物

1-D 依赖输入数据数组，长度与 x 相同。

w(N,) 数组类似物（可选）

样条拟合权重。必须为正数。如果 w 为 None，那么所有权重均为 1。默认为 None。

bbox(2,) array_like, optional

2 序列，用于指定逼近区间的界限。如果 bbox 为 None，则 bbox=[x[0], x[-1]]。默认为 None。

kint, optional

平滑样条的度数。必须满足 1 <= k <= 5。 k = 3 表示三次样条。默认为 3。

sfloat or None, optional

用于选择节点数目的正平滑因子。节点数目将增加，直至满足平滑条件。

sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s

然而，出于数字问题，实际条件是

abs(sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) - s) < 0.001 * s

如果 s 为 None，则将 s 设置为 len(w)，以使用所有数据点的平滑样条。如果是 0，则样条将通过所有数据点进行内插。这等于 InterpolatedUnivariateSpline。默认为 None。用户可以使用 s 来控制拟合的紧密性和平滑度之间的权衡。s 越大，平滑度越高，而 s 的值越小，则平滑度越低。s 的建议值取决于权重 w。如果权重表示 y 的标准差的倒数，则可以在 ( m - sqrt( 2 * m ) , m + sqrt( 2 * m ) ) 范围内找到一个合适的 s 值，其中 m 是 x、y 和 w 中的数据点数量。这意味着，如果 1/w[i] 是 y[i] 标准差的估计，则 s = len(w) 应该是一个合适的值。

extint or str, optional

控制节点序列定义的区间之外元素的外推模式。

如果 ext=0 或 ‘extrapolate’，则返回外推值。
如果 ext=1 或 ‘zeros’，则返回 0。
如果 ext=2 或 ‘raise’，则引发 ValueError。
如果 ext=3 或 ‘const’，则返回边界值。

默认为 0。

check_finitebool, optional

是否检查输入阵列是否只包含有限数字。禁用可能会获得性能提升，但如果输入包含无穷大或 NaN，可能会导致问题（崩溃、不终止或无意义的结果）。默认设置为 False。

另请参见

BivariateSpline: bivariate 样条函数的基本类。
SmoothBivariateSpline: 通过给定点实现平滑 bivariate 样条函数
LSQBivariateSpline: 使用加权最小二乘拟合的 bivariate 样条函数
RectSphereBivariateSpline: 球体上矩形网格上的 bivariate 样条函数
SmoothSphereBivariateSpline: 球坐标系中的平滑 bivariate 样条函数
LSQSphereBivariateSpline: 使用加权最小二乘拟合的球坐标系中的 bivariate 样条函数
RectBivariateSpline: 矩形网格上的 bivariate 样条函数
InterpolatedUnivariateSpline: 给定一组数据点用于插值的 univariate 样条函数。
bisplrep: 用于查找曲面的 bivariate B 样条函数表示形式的函数
bisplev: 用于计算 bivariate B 样条函数及其导数的函数
splrep: 用于查找一维曲线的 B 样条函数表示形式的函数
splev: 用于计算 B 样条函数或其导数的函数
sproot: 用于查找三次 B 样条函数根的函数
splint: 用于计算给定两个点之间 B 样条函数定积分的函数
spalde: 用于计算 B 样条函数所有导数的函数

说明

数据点数量必须大于样条函数次数k。

NaN 处理：如果输入阵列包含nan值，则结果无用，因为基础样条函数拟合例程无法处理nan。解决方法是对无效数字数据点使用零权重

>>> import numpy as np
>>> from scipy.interpolate import UnivariateSpline
>>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4])
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> spl = UnivariateSpline(x, y, w=~w)

请注意需要将nan替换为数值（只要相应的权重为零，则精确值无关紧要）。

参考文献

基于 [1]、[2]、[3] 和 [4] 中所述的算法

[1]

P. Dierckx，“使用样条函数进行实验数据平滑、微分和积分的算法”，J.Comp.Appl.Maths 1 (1975) 165-184。

[2]

P. Dierckx，“使用样条函数对矩形网格上的数据进行平滑的快速算法”，SIAM J.Numer.Anal. 19 (1982) 1286-1304。

[3]

P. Dierckx，“使用样条函数进行曲线拟合的改进算法”，报告 tw54，比利时鲁汶大学计算机科学系，1981 年。

[4]

P. Dierckx，"曲线和曲面样条拟合"，数值分析专著，牛津大学出版社，1993。

示例

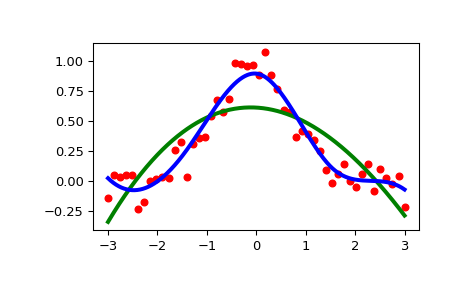
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import UnivariateSpline
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
>>> plt.plot(x, y, 'ro', ms=5)

对平滑参数使用默认值

>>> spl = UnivariateSpline(x, y)
>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(xs, spl(xs), 'g', lw=3)

手动更改平滑量

>>> spl.set_smoothing_factor(0.5)
>>> plt.plot(xs, spl(xs), 'b', lw=3)
>>> plt.show()

../../_images/scipy-interpolate-UnivariateSpline-1.png

方法

`__call__`(x[, nu, ext])	在位置 x 中计算样条（或其第 nu 阶导数）。
`antiderivative`([n])	构造一条表示此样条的导函数的新样条。
`derivative`([n])	构造一条表示此样条的导数的新样条。
`derivatives`(x)	返回在点 x 处样条的所有导数。
`get_coeffs`()	返回样条系数。
`get_knots`()	获取样条内部结的位置。
`get_residual`()	返回样条近似的加权平方残差总和。
`integral`(a, b)	返回两个给定点之间样条的定积分。
`roots`()	返回样条的零点。
`set_smoothing_factor`(s)	使用给定的平滑系数 s 和在上次调用中找到的结，继续样条计算。

validate_input