scipy.stats.

rv_histogram

class scipy.stats.rv_histogram(histogram, *args, density=None, **kwargs)

生成由直方图给定的分布。这对于从分箱数据样本生成模板分布很有用。

作为 rv_continuous 类的子类，rv_histogram 从它继承了一组通用方法（请参阅 rv_continuous 获取完整列表），并根据提供的分箱数据样本的属性实现它们。

参数:

histogramarray_like 类型的元组

包含两个 array_like 对象的元组。第一个包含 n 个 bin 的内容，第二个包含 (n+1) 个 bin 边界。特别是，接受 numpy.histogram 的返回值。

densitybool, 可选

如果为 False，则假定直方图与每个 bin 的计数成正比；否则，假定它与 bin 上的密度成正比。对于恒定的 bin 宽度，这些是等效的，但当 bin 宽度变化时，这种区别很重要（请参阅注释）。如果为 None（默认），则为了向后兼容性设置 density=True，但如果 bin 宽度可变，则发出警告。显式设置 density 以消除警告。

在 1.10.0 版本中添加。

属性:

random_state

获取或设置用于生成随机变量的生成器对象。

方法

__call__(*args, **kwds)	为给定的参数冻结分布。
cdf(x, *args, **kwds)	给定 RV 的累积分布函数。
entropy(*args, **kwds)	RV 的微分熵。
expect([func, args, loc, scale, lb, ub, ...])	通过数值积分计算函数关于分布的期望值。
fit(data, *args, **kwds)	从数据返回形状（如果适用）、位置和比例参数的估计值。
fit_loc_scale(data, *args)	使用一阶和二阶矩从数据估计 loc 和 scale 参数。
freeze(*args, **kwds)	为给定的参数冻结分布。
interval(confidence, *args, **kwds)	围绕中位数的等面积置信区间。
isf(q, *args, **kwds)	给定 RV 的 q 处的逆生存函数（sf 的逆）。
logcdf(x, *args, **kwds)	给定 RV 的 x 处的累积分布函数的对数。
logpdf(x, *args, **kwds)	给定 RV 的 x 处的概率密度函数的对数。
logsf(x, *args, **kwds)	给定 RV 的生存函数的对数。
mean(*args, **kwds)	分布的均值。
median(*args, **kwds)	分布的中位数。
moment(order, *args, **kwds)	指定阶数的分布的非中心矩。
nnlf(theta, x)	负对数似然函数。
pdf(x, *args, **kwds)	给定 RV 的 x 处的概率密度函数。
ppf(q, *args, **kwds)	给定 RV 的 q 处的分位数函数（cdf 的逆）。
rvs(*args, **kwds)	给定类型的随机变量。
sf(x, *args, **kwds)	给定 RV 的 x 处的生存函数 (1 - cdf)。
stats(*args, **kwds)	给定 RV 的一些统计量。
std(*args, **kwds)	分布的标准差。
support(*args, **kwargs)	分布的支持。
var(*args, **kwds)	分布的方差。

注释

当直方图具有不相等的 bin 宽度时，与每个 bin 的计数成正比的直方图和与 bin 上的概率密度成正比的直方图之间存在区别。如果调用 numpy.histogram 及其默认 density=False，则生成的直方图是每个 bin 的计数数，因此应将 density=False 传递给 rv_histogram。如果调用 numpy.histogram 并使用 density=True，则生成的直方图采用概率密度形式，因此应将 density=True 传递给 rv_histogram。为避免警告，当输入直方图具有不相等的 bin 宽度时，请始终显式传递 density。

除了 loc 和 scale 之外，没有其他形状参数。pdf 被定义为来自提供的直方图的逐步函数。cdf 是 pdf 的线性插值。

在 0.19.0 版本中添加。

示例

在您的浏览器中尝试一下！

从 numpy 直方图创建一个 scipy.stats 分布

>>> import scipy.stats
>>> import numpy as np
>>> data = scipy.stats.norm.rvs(size=100000, loc=0, scale=1.5,
...                             random_state=123)
>>> hist = np.histogram(data, bins=100)
>>> hist_dist = scipy.stats.rv_histogram(hist, density=False)

行为类似于普通的 scipy rv_continuous 分布

>>> hist_dist.pdf(1.0)
0.20538577847618705
>>> hist_dist.cdf(2.0)
0.90818568543056499

PDF 在直方图的最高（最低）bin 之上（之下）为零，由原始数据集的最大值（最小值）定义

>>> hist_dist.pdf(np.max(data))
0.0
>>> hist_dist.cdf(np.max(data))
1.0
>>> hist_dist.pdf(np.min(data))
7.7591907244498314e-05
>>> hist_dist.cdf(np.min(data))
0.0

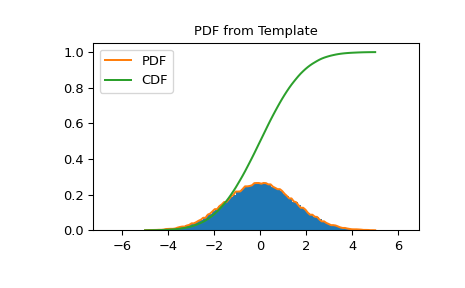
PDF 和 CDF 遵循直方图

>>> import matplotlib.pyplot as plt
>>> X = np.linspace(-5.0, 5.0, 100)
>>> fig, ax = plt.subplots()
>>> ax.set_title("PDF from Template")
>>> ax.hist(data, density=True, bins=100)
>>> ax.plot(X, hist_dist.pdf(X), label='PDF')
>>> ax.plot(X, hist_dist.cdf(X), label='CDF')
>>> ax.legend()
>>> fig.show()

返回在新标签页中打开