scipy.signal.

max_len_seq#

scipy.signal.max_len_seq(nbits, state=None, length=None, taps=None)[source]#

最大长度序列 (MLS) 生成器。

参数:

nbitsint: 要使用的比特数。生成序列的长度将为 (2**nbits) - 1。请注意，生成长序列（例如，大于 nbits == 16）可能需要很长时间。
statearray_like, optional: 如果为数组，则长度必须为 nbits，并将转换为二进制 (bool) 表示。如果为 None，将使用全一的种子，生成可重复的表示。如果 state 全为零，则会引发错误，因为这是无效的。默认值：None。
lengthint, optional: 要计算的样本数。如果为 None，则计算整个长度 (2**nbits) - 1。
tapsarray_like, optional: 要使用的多项式抽头（例如，8 位序列的 [7, 6, 1]）。如果为 None，将自动选择抽头（最多 nbits == 32）。

返回:

seqarray: 生成的由 0 和 1 组成的 MLS 序列。
statearray: 移位寄存器的最终状态。

备注

MLS 生成算法在以下链接中通用描述：

https://zh.wikipedia.org/wiki/最大长度序列

抽头的默认值特别取自以下链接中每个 nbits 值的第一个选项：

https://web.archive.org/web/20181001062252/http://www.newwaveinstruments.com/resources/articles/m_sequence_linear_feedback_shift_register_lfsr.htm

自 0.15.0 版本加入。

示例

MLS 使用二进制约定

>>> from scipy.signal import max_len_seq
>>> max_len_seq(4)[0]
array([1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int8)

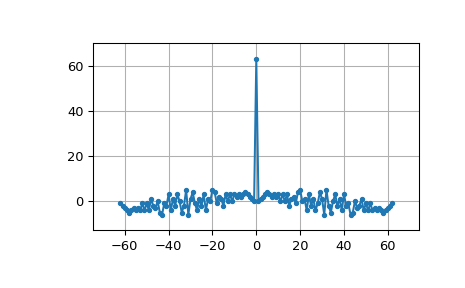
MLS 具有白频谱（直流除外）

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1  # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
>>> plt.plot(fftshift(fftfreq(N)), fftshift(np.abs(spec)), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

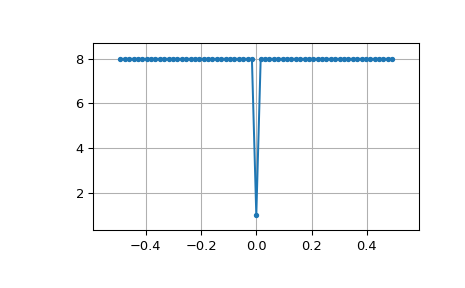
../../_images/scipy-signal-max_len_seq-1_00_00.png

MLS 的循环自相关是脉冲

>>> acorrcirc = ifft(spec * np.conj(spec)).real
>>> plt.figure()
>>> plt.plot(np.arange(-N/2+1, N/2+1), fftshift(acorrcirc), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

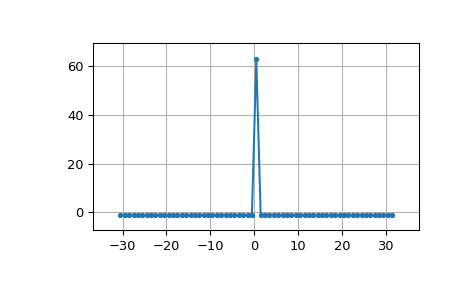
../../_images/scipy-signal-max_len_seq-1_01_00.png

MLS 的线性自相关近似为脉冲

>>> acorr = np.correlate(seq, seq, 'full')
>>> plt.figure()
>>> plt.plot(np.arange(-N+1, N), acorr, '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-max_len_seq-1_02_00.png