特殊函数 (scipy.special)#

包 scipy.special 的主要功能是对数学物理中的许多特殊函数的定义。提供的函数包括艾里函数、椭圆函数、贝塞尔函数、伽马函数、贝塔函数、超几何函数、抛物柱函数、马蒂厄函数、球面波函数、斯特鲁夫函数和开尔文函数。还有一些低级别的统计函数，不打算供一般用途使用，因为 stats 模块提供了到这些函数的一个更简单的界面。大多数这些函数都可以使用数组参数并返回数组结果，遵循与数值 Python 中其他数学函数相同的广播规则。其中许多函数还接收复数作为输入。要获取带有单行描述的可用函数的完整列表，请键入 >>> help(special). 每个函数还有自己的文档，可以使用 help 访问。如果您没有看到您需要的功能，请考虑编写它并将其贡献给该库。您可以在 C、Fortran 或 Python 中编写该函数。在库的源代码中查找每种类型的函数的示例。

实阶贝塞尔函数 (jv, jn_zeros) #

贝塞尔函数是一族满足带有实数或复数阶数 alpha 的贝塞尔微分方程的解

\[x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]

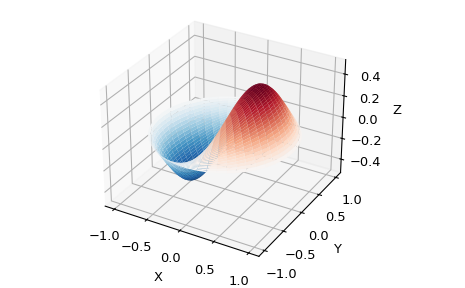
除其他用途外，这些函数出现在波传播问题中，例如薄鼓头的振动模式。下面是边缘固定的圆鼓头的例子

>>> from scipy import special
>>> import numpy as np
>>> def drumhead_height(n, k, distance, angle, t):
...    kth_zero = special.jn_zeros(n, k)[-1]
...    return np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero)
>>> theta = np.r_[0:2*np.pi:50j]
>>> radius = np.r_[0:1:50j]
>>> x = np.array([r * np.cos(theta) for r in radius])
>>> y = np.array([r * np.sin(theta) for r in radius])
>>> z = np.array([drumhead_height(1, 1, r, theta, 0.5) for r in radius])

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_axes(rect=(0, 0.05, 0.95, 0.95), projection='3d')
>>> ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='RdBu_r', vmin=-0.5, vmax=0.5)
>>> ax.set_xlabel('X')
>>> ax.set_ylabel('Y')
>>> ax.set_xticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_yticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_zlabel('Z')
>>> plt.show()
"This code generates a 3-D representation of the vibrational modes on a drum head viewed at a three-quarter angle. A circular region on the X-Y plane is defined with a Z value of 0 around the edge. Within the circle a single smooth valley exists on the -X side and a smooth peak exists on the +X side. The image resembles a yin-yang at this angle."

特殊函数的 Cython 绑定 (scipy.special.cython_special) #

SciPy 还为特殊中的许多函数提供标量、类型化版本的 Cython 绑定。下面的 Cython 代码给出了如何使用这些函数的一个简单示例

cimport scipy.special.cython_special as csc

cdef:
    double x = 1
    double complex z = 1 + 1j
    double si, ci, rgam
    double complex cgam

rgam = csc.gamma(x)
print(rgam)
cgam = csc.gamma(z)
print(cgam)
csc.sici(x, &si, &ci)
print(si, ci)

（有关编译 Cython 的帮助，参见 Cython 文档。）在示例中，函数 csc.gamma 基本工作原理与 ufunc 对应项 gamma 类似，尽管它将 C 类型作为参数接受，而不是 NumPy 数组。尤其是需要注意，函数被重载以支持实数和复数参数；在编译时选择正确的变种。函数 csc.sici 的工作原理与 sici 稍有不同；对于 ufunc，我们可以编写 ai, bi = sici(x)，而在 Cython 版本中，将多个返回值作为指针传递。将其视为类似于使用输出数组调用 ufunc 可能会对您有所帮助：sici(x, out=(si, ci))。

使用 Cython 绑定的潜在优势有以下两点

  • 它们避免 Python 函数开销

  • 它们不需要 Python 全局解释器锁 (GIL)

以下部分讨论如何利用这些优势来加快代码速度，当然，您应该始终先分析代码，以确保做好额外工作是值得的。

避免 Python 函数开销#

对于 special 中的 ufunc，避免 Python 函数开销的方法是矢量化，即向函数传递数组。通常，此方法的效果很好，但有时在循环内对标量输入调用特殊函数更加方便，例如在您实现自己的 ufunc 时。在这种情况下，Python 函数开销可能会变得显著。考虑以下示例：

import scipy.special as sc
cimport scipy.special.cython_special as csc

def python_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        sc.jv(n, x)

def cython_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        csc.jv(n, x)

在一台计算机上，python_tight_loop 花费大约 131 微秒来运行，cython_tight_loop 花费大约 18.2 微秒来运行。显而易见，此示例是人为设计的：您直接调用 special.jv(np.arange(100), 1) 即可获得与 cython_tight_loop 中一样快的结果。关键是，如果 Python 函数开销在您的代码中变得显著，那么 Cython 绑定可能会很有用。

释放 GIL#

通常，人们需要在很多点评估特殊函数，而且这些评估通常可以轻松并行化。由于 Cython 绑定不需要 GIL，因此可以使用 Cython 的 prange 函数，轻松地并行运行这些函数。例如，假设我们希望计算 Helmholtz 方程的基础解

\[\Delta_x G(x, y) + k^2G(x, y) = \delta(x - y),\]

其中 \(k\) 是波数，\(\delta\) 是狄拉克 delta 函数。已知在二维中唯一的（辐射）解为

\[G(x, y) = \frac{i}{4}H_0^{(1)}(k|x - y|),\]

其中 \(H_0^{(1)}\) 是第一类汉克尔函数，即函数 hankel1。以下示例演示了我们如何在并行计算中计算此函数

from libc.math cimport fabs
cimport cython
from cython.parallel cimport prange

import numpy as np
import scipy.special as sc
cimport scipy.special.cython_special as csc

def serial_G(k, x, y):
    return 0.25j*sc.hankel1(0, k*np.abs(x - y))

@cython.boundscheck(False)
@cython.wraparound(False)
cdef void _parallel_G(double k, double[:,:] x, double[:,:] y,
                      double complex[:,:] out) nogil:
    cdef int i, j

    for i in prange(x.shape[0]):
        for j in range(y.shape[0]):
            out[i,j] = 0.25j*csc.hankel1(0, k*fabs(x[i,j] - y[i,j]))

def parallel_G(k, x, y):
    out = np.empty_like(x, dtype='complex128')
    _parallel_G(k, x, y, out)
    return out

（有关在 Cython 中编译并行代码的帮助，请参见 此处。）如果上述 Cython 代码位于文件 test.pyx 中，那么我们就可以编写一个非正式基准，对函数的并行和串行版本进行比较

import timeit

import numpy as np

from test import serial_G, parallel_G

def main():
    k = 1
    x, y = np.linspace(-100, 100, 1000), np.linspace(-100, 100, 1000)
    x, y = np.meshgrid(x, y)

    def serial():
        serial_G(k, x, y)

    def parallel():
        parallel_G(k, x, y)

    time_serial = timeit.timeit(serial, number=3)
    time_parallel = timeit.timeit(parallel, number=3)
    print("Serial method took {:.3} seconds".format(time_serial))
    print("Parallel method took {:.3} seconds".format(time_parallel))

if __name__ == "__main__":
    main()

在一台四核计算机上，串行方法花费了 1.29 秒，而并行方法花费了 0.29 秒。

scipy.special 中未包含的函数#

有些函数未包含在 special 中，这是因为使用 NumPy 和 SciPy 中的现有函数可轻松实现这些函数。为了避免重复造轮子，本部分提供了几个此类函数的实现，希望这些函数可以说明如何处理类似函数。在所有示例中，NumPy 导入为 np，special 导入为 sc。

二进制熵函数

def binary_entropy(x):
    return -(sc.xlogy(x, x) + sc.xlog1py(1 - x, -x))/np.log(2)

[0, 1] 上的矩形阶跃函数

def step(x):
    return 0.5*(np.sign(x) + np.sign(1 - x))

可以使用平移和缩放来实现任意阶跃函数。

斜坡函数

def ramp(x):
    return np.maximum(0, x)
此页面上的内容